题目内容
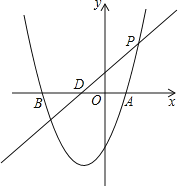
【题目】如图，抛物线y＝x2+bx+c与x轴交于A（1，0），B（﹣3，0），与y轴交于C．
（1）求该抛物线的解析式，并写出抛物线的对称轴；
（2）设抛物线的对称轴交x轴于D，在对称轴左侧的抛物线上有一点E，使S△ACE＝
，求点E的坐标；
（3）若P是直线y＝x+1上的一点，P点的横坐标为
，M是第二象限抛物线上的一点，当∠MPD＝∠ADC时，求M点的坐标．
【答案】（1）y＝x2+2x﹣3．（2）E（﹣4，5）．（3）M（﹣4，5）
【解析】
（1）根据待定系数法确定二次函数的解析式即可；
（2）根据E点在抛物线上，设E（m，m2+2m﹣3），再结合已知条件，利用三角形的面积计算公式S=
底
高，从而解得m的值；
（3）首先过点D作DN⊥DP，交PM的延长线与点N，过点N作NL⊥x轴，过点P作PE⊥x轴，再利用已知条件证明△NPD∽△CDO，同时证明△NLD∽△DEP，因此得到N点坐标，N点在一次函数上，可以得到一次函数的解析式，根据M点是一次函数和二次函数的交点，联立方程组，解得M点的坐标，已知M点在第二象限上删去不符合条件的M点的坐标。
解：（1）∵A（1，0），B（﹣3，0）关于直线x＝﹣1对称，
∴抛物线的对称轴为x＝﹣1．
抛物线的解析式为y＝（x﹣1）（x+3）＝x2+2x﹣3．
（2）设点E（m，m2+2m﹣3）．
∵AD＝2，OC＝3，
∴S△ACD＝
×ADOC＝3．
∵S△ACE＝
，
∴S△ACE＝10．
设直线AE的解析式为y＝kx﹣b．把点A和点E的坐标代入得：
，解得：
．
∴直线AE的解析式为y＝（m+3）x﹣m﹣3．
∴F（0，﹣m﹣3）．
∵C（0，﹣3），
∴FC＝﹣m﹣3+3＝﹣m．
∴S△EAC＝
×FC×（1﹣m）＝10，即﹣m（1﹣m）＝20，解得：m＝﹣4或m＝5（舍去）．
∴E（﹣4，5）．
（3）如图所示：
过点D作DN⊥DP，交PM的延长线与点N，过点N作NL⊥x轴，垂足为L，过点P作PE⊥x轴，垂足为E．
∵∠MPD＝∠ADC，∠NDP＝∠DOC，
∴△NPD∽△CDO．
∴
＝
，
∴
＝
＝3．
又∵△NLD∽△DEP，
∴
＝
＝
＝3，
∴NL＝7，DL＝7，
∴N（﹣8，7）．
∴直线PN的解析式为y＝﹣
x﹣3．
联立y＝x2+2x﹣3与y＝﹣x﹣3，解得：x＝
（舍去）或x＝﹣4．
∴M（﹣4，5）．
