题目内容

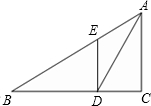如图，Rt△ABC中，∠C=90°，AD为∠BAC的角平分线，DE∥AC交AB于E，且AD=2，AC= $数学公式$ ．
（1）求∠B的度数；
（2）求S_△ADE：S_△ADC？

解：（1）在Rt△ACD中，
sin∠ADC= $\text{[math]}$ = $\text{[math]}$ ，
∴∠ADC=60°，
∴∠CAD=30°，
又AD为∠BAC的角平分线，所以得∠BAC=60°，
∴∠B=30°；

（2）在Rt△ACD中，∠CAD=30°，
∴CD= $\text{[math]}$ AD=1，
∴S_△ADC= $\text{[math]}$ AC•CD= $\text{[math]}$ × $\text{[math]}$ ×1= $\text{[math]}$ ，
过点E作EF⊥AD交AD于F，

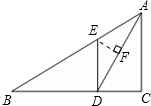∵DE∥AC，
∴∠EDA=∠CAD=∠EAD=30°，
∴△EDA为等腰三角形，
∴AF=DF=1，
∴EF=DF•tan30°=1× $\text{[math]}$ ，
∴S_△ADE= $\text{[math]}$ AD•EF= $\text{[math]}$ ×2× $\text{[math]}$ = $\text{[math]}$ ，
∴S_△ADE：S_△ADC= $\text{[math]}$ ： $\text{[math]}$ =2：3．
分析：（1）由已知AD=2，AC= $\text{[math]}$ ，在Rt△ACD中，可求出∠ADC=60°，即得∠CAD=30°，又AD为∠BAC的角平分线，所以得∠BAC=60°，从而求出∠B=30°；
（2）在Rt△ACD中，可求出CD，即可求出三角形ACD的面积，再过点E作EF⊥AD交AD于F，由DE∥AC得△EDA为等腰三角形，从而求出EF，则求出三角形ADE的面积，即得答案．
点评：此题考查的知识点是解直角三角形，关键是运用直角三角形三角函数及角平分线性质求出∠B，再由平行线性质得等腰三角形及三角函数求出EF．