题目内容
 Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=
Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=| k |
| x |
| A、5 | B、8 | C、-10 | D、-15 |
考点:反比例函数系数k的几何意义
专题:
分析:设OA=a,AE=b,则C点坐标(a,
),B点坐标(b,
)根据S△BCD=S△ACD=5,得出S△ACB=10=
AC•BC=
•(-
)b得出bk=-20a①,先求得D的坐标,根据点D在抛物线上,得出(
b+a)(
•
)=k,则b=2a②,结合①②,即可求得k的值.
| k |
| a |
| k |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| a |
解答: 解:设OA=a,AE=b,则C点坐标(a,
解:设OA=a,AE=b,则C点坐标(a,
),B点坐标(a+b,
)
∵AD=BD,
∴S△BCD=S△ACD=5,
∴S△ACB=10=
AC•BC=
•(-
)•b
得bk=-20a,
∵B点坐标(a+b,
)
∴点D在抛物线上,D点坐标(
b+a,
*
)
则(
b+a)(
•
)=k,
则b=2a,
解
得k=-10.
故答案为-10.
 解:设OA=a,AE=b,则C点坐标(a,
解:设OA=a,AE=b,则C点坐标(a,| k |
| a |
| k |
| a |
∵AD=BD,
∴S△BCD=S△ACD=5,
∴S△ACB=10=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| a |
得bk=-20a,
∵B点坐标(a+b,
| k |
| a |
∴点D在抛物线上,D点坐标(
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| a |
则(
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| a |
则b=2a,
解
|
故答案为-10.
点评:本题考查了反比例函数系数k的几何意义:三角形的面积等于
|k|.
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
⊙O的半径为4,圆心到点P的距离为d,且d是方程x2-2x-8=0的根,则点P与⊙O的位置关系是( )
| A、点P在⊙O内部 |
| B、点P在⊙O上 |
| C、点P在⊙O外部 |
| D、点P不在⊙O上 |
一个圆锥的母线长为8,侧面展开图是半圆,则这个圆锥的高是( )
| A、4 | ||
B、4
| ||
C、4
| ||
D、2
|
下列命题中:(1)零是正数;(2)零是整数;(3)零是最小的有理数;(4)零是非负数;(5)零是偶数,正确命题的个数是( )
| A、2个 | B、3个 | C、4个 | D、5个 |
A、B两地相距a千米,甲每小时行x千米,乙的速度是甲的1.2倍,甲、乙两人分别从A、B两地同时出发,相向而行,则他们相遇所需要的时间是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、(
|
如果一个多项式是五次多项式,那么( )
| A、这个多项式至少有一项的次数是5 |
| B、这个多项式只能有一项的次数是5 |
| C、这个多项式一定是五次六项式 |
| D、这个多项式最多有六项 |
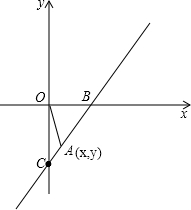 如图,y=2x-1与x轴、y轴分别交于B、C两点,点A(x,y)是第四象限内的直线y=2x-1上的一个动点.
如图,y=2x-1与x轴、y轴分别交于B、C两点,点A(x,y)是第四象限内的直线y=2x-1上的一个动点.