Question

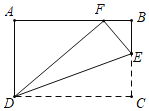
【题目】如图，在矩形中，，点在上，且，连接，将矩形沿直线翻折，点恰好落在上的点处，则__________．

Answer 1

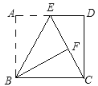
【答案】16

【解析】

由题意易证得△FBC≌△DCE（AAS），BC＝AD，FB＝AB＝CD=30，然后设FC＝x，在Rt△FBC中，由勾股定理可得BC2＝FB2＋FC2，即可得方程，解方程即可求得答案．

解：∵四边形ABCD是矩形，

∴AB＝CD＝30，∠A＝∠D＝90°，AD∥BC，AD＝BC，

∴∠DEC＝∠FCB，

由折叠的性质，得：FB＝AB＝30，∠BFE＝∠A＝90°，

∴FB＝CD，∠BFC＝∠D＝90°，

在△FBC和△DCE中，

，

∴△FBC≌△DCE（AAS），

∴FC＝DE，

设FC＝x，则BC＝AD＝DE＋AE＝x＋18

在Rt△FBC中，BC2＝FB2＋FC2，

即（x＋18）2＝x2＋302，

解得：x＝16，

∴AF＝16．

故答案为：16．