题目内容
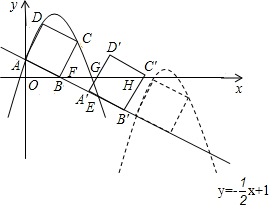
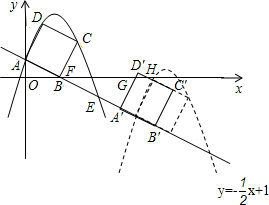
如图,已知直线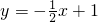 分别交y轴、x轴于A,B两点,以线段AB为边向上作正方形ABCD过点A,D,C的抛物线y=ax2+bx+1与直线的另一交点为点E
分别交y轴、x轴于A,B两点,以线段AB为边向上作正方形ABCD过点A,D,C的抛物线y=ax2+bx+1与直线的另一交点为点E
(1)点C的坐标为______;点D的坐标为______.并求出抛物线的解析式;
(2)若正方形以每秒 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
(3)在(2)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.

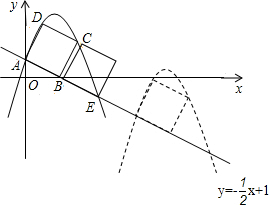 解:(1)∵A在y轴上,B在x轴上,则
解:(1)∵A在y轴上,B在x轴上,则A(0,1),B(2,0)
C(3,2),D(1,3)
过点A,D,C的抛物线:y=-
 x2+
x2+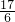 x+1
x+1与直线交点为A(0,1),E(4,-1)
所以点E坐标为(4,-1);
(2)①当点A运动到点B时,t=1,当0<t≤1时,
∵∠OBA=∠GBB′,
tan∠OBA=
 =
= ,
,∴tan∠GFB′=
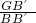 =
=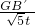 =
= ,
,∴GB′=
 t,
t,∴S△BB′G=
 BB′×GB′=
BB′×GB′= ×
× t×
t× t=
t= t2;
t2;②当点C运动到x轴t=2,
当1<t≤2时,
A′B′=AB=
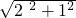 =
= ,
,∴A′F=
 t-
t- ,
,∴A′G=
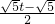 ,
,
∵B′H=
 t,
t,∴S梯形A′B′HG=
 (A′G+B′H)×A′B′,
(A′G+B′H)×A′B′,=
 (
(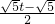 +
+ t)×
t)× ,
,=
 -
- ;
;③当点D运动到x轴上时,t=3,当2<t≤3时,
∵A′G=
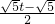 ,∴GD′=
,∴GD′= -
-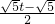 =
=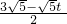 ,
,∵S△AOF=
 ×1×2=1,OA=1,
×1×2=1,OA=1,∵△AOF∽△GD′H,
∴
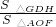 =(
=(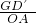 )2,
)2,∴S△GD′H=(
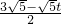 )2,
)2,∴S五边形GA′B′C′H=(
 )2-(
)2-(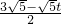 )2=
)2= t2+
t2+ t-
t- ;
;(3)∵t=3,BB′=AA′=3
 ,
,∴S阴影=S矩形BB′C′C=S矩形AA′D′D=AD×AA′=
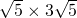 =15.
=15.分析:(1)由正方形的性质,可直接求出C,D的坐标,然后可求出抛物线解析式;
(2)动点问题的解决应找到特殊分界点进行讨论,当点A运动到点F时,t=1,当0<t≤1时,当点C运动到x轴t=2,当点D运动到x轴上时,t=3,当2<t≤3时,分别得出函数解析式;
(3)根据阴影部分比较特殊,可以转化为矩形的面积,从而求出.
点评:此题主要考查二次函数解析式的求法,以及动点问题,动点问题的解决关键是找到特殊分界点,进行讨论是解决问题的关键,此题综合性较强,分析过程中必须细心.

练习册系列答案
相关题目
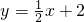 分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.
分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD. 抛物线y=ax2+bx+c经过A、C、D三点.
抛物线y=ax2+bx+c经过A、C、D三点. 分别交y轴、x轴于A,B两点,以线段AB为边向上作正方形ABCD过点A,D,C的抛物线y=ax2+bx+1与直线的另一交点为点E
分别交y轴、x轴于A,B两点,以线段AB为边向上作正方形ABCD过点A,D,C的抛物线y=ax2+bx+1与直线的另一交点为点E 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
 分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.抛物线y=ax2+bx+c经过A、C、D三点.
分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.抛物线y=ax2+bx+c经过A、C、D三点.
 分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.抛物线y=ax2+bx+c经过A、C、D三点.
分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.抛物线y=ax2+bx+c经过A、C、D三点.
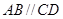 ,直线
,直线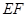 分别交
分别交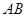 、
、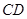 于点
于点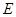 、
、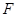 ,过
,过 于点
于点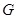 。若
。若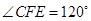 ,则
,则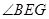 的大小为( )
的大小为( )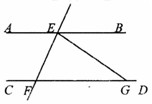
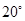 B.
B.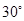 C.
C.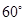 D.
D.