��Ŀ����
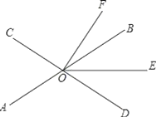
����Ŀ����ͼ������AM��BN����E��F��D������AM�ϣ���C������BN�ϣ��ҡ�BCD����A��BEƽ�֡�ABF��BDƽ�֡�FBC.
(1)��֤��AB��CD.
(2)���ƽ���ƶ�CD����ô��AFB���ADB�ı�ֵ�Ƿ����仯�����仯���ҳ��仯���ɣ������䣬����������ǵı�ֵ��
(3)�����A��100������ô��ƽ���ƶ�CD�Ĺ����У��Ƿ����ijһʱ�̣�ʹ��AEB����BDC�������ڣ������ʱ��AEB�Ķ������������ڣ���˵�����ɣ�

���𰸡���1��֤������������2������,���ɼ���������3������,60��
��������
��1������ƽ���ߵ����ʣ��Լ���������֤����A+��ABC=180����Ȼ���֤��AB��CD��
��2��������������ǵ����ʿ�ֱ�ӵó����ۣ�
��3������ƽ���ߵ����ʵõ���ABC=80�������CBD=��FBD=��FDB=x�������ݽ�ƽ���ߵ����ʵõ���EBD=40�������ǵõ���AEB=x��+40�����õ���BDC=80��-x�������ݡ�AFC=��ADB���з��̼��ɵõ����ۣ�
��1��֤������AM��BN��
���A+��ABC=180����
�֡ߡ�BCD=��A��
���ABC+��BCD=180����
��AB��CD��
��2����AM��BN�����ADB=��DBC����BDƽ�֡�FBC�����FBD=��DBC��
���FBD=��FDB��
��CD����ƽ��ʱ����FBD����ABC���䣬
�ߡ�FBD=��FDB����BFA=��FBD+��FDB�����AFB����ADB=2��1��
��3�����ڣ�
���ɣ��ߡ�A=100�������ABC=80����
���CBD=��FBD=��FDB=x����
��BEƽ�֡�ABF��BDƽ�֡�FBC��
���EBD=40��
���AEB=x��+40����
��AM��BN����BCD=100����
���CDA=80����
���BDC=80��-x����
�ߡ�AEB=��BDC��
��x��+40��=80��-x�������x=20����
���AEB=20��+40��=60����

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�