题目内容
【题目】有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．
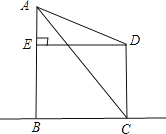
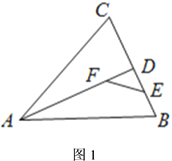
(1)如图1，在
中，
，
是的角平分线，
，
分别是
，上的点．求证：四边形
是邻余四边形；
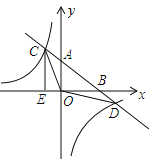
(2)如图2，已知，点
在
的垂直平分线上，
在边上，
是内一点， 连接
，
，
，
，若四边形
是邻余四边形，
是邻余线.
①与
有什么位置关系？说明理由．
②判断形状，说明理由.
【答案】(1)证明见解析；(2)①
；②
是等边三角形.
【解析】
（1）方法1：通过等腰三角形三线合一得到
，
，进而得到
与
互余，即得证.方法2：由等腰三角形性质得到
，由角平分线性质得到
，进而得到
，即得证；（2）①根据邻余四边形性质可得到∠B=60°，与∠AED相等，故；②由垂直平分线性质得到AB=AC，又∠B=60°，故△ABC为等边三角形.
解：(1)方法1：
，
是的角平分线，
，
，
，
与互余.
四边形
是邻余四边形；
方法2：，
，
是的角平分线，
，
四边形是邻余四边形；
(2)①.
理由：
四边形
是邻余四边形，
是邻余线，
，
，
，
，
②是等边三角形.
理由：点
在
的垂直平分线上，
，
又
，
是等边三角形.
练习册系列答案
相关题目
