Question

已知x₁，x₂是一元二次方程x²+x+n=0的两个实数根，且x₁²+x₂²+（x₁+x₂）²=3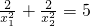，，则m=________n=________．

Answer 1

    -1
分析：由x₁，x₂是一元二次方程x²+x+n=0的两个实数根，利用根与系数的关系表示出x₁+x₂与x₁x₂，且得到根的判别式大于等于0，得到m大于4n，将已知的两等式变形后代入得到关于m与n的方程组，求出方程组的解即可得到m与n的值．
解答：∵x₁，x₂是一元二次方程x²+x+n=0的两个实数根，
∴x₁+x₂=-，x₁x₂=n，b²-4ac=m-4n≥0，即m≥4n，
化简得：x₁²+x₂²+（x₁+x₂）²=2（x₁+x₂）²-2x₁x₂=2m-2n=3①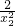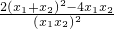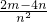，+===5②，
由①得：2m=2n+3③，
③代入②整理得：（5n-3）（n+1）=0，解得：n=或-1，
当n=时，m=（不合题意，舍去）；当n=-1时，m=，
则m=，n=-1．
故答案为：；-1
点评：此题考查了一元二次方程根与系数的关系，一元二次方程ax²+bx+c=0（a≠0），当b²-4ac≥0时，方程有解，设两根分别为x₁，x₂，则有x₁+x₂=-，x₁x₂=．