题目内容
如图,在Rt△ABC中,∠C=90,点D在AC边上.若DB=6, AD=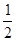 CD,sin∠CBD=
CD,sin∠CBD=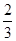 ,求AD的长和tanA的值.
,求AD的长和tanA的值.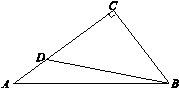
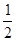 CD,sin∠CBD=
CD,sin∠CBD=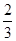 ,求AD的长和tanA的值.
,求AD的长和tanA的值.
AD=2,tanA=2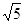
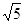
试题分析:∵sin∠CBD=
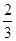 ∠C=90°BD=6∴sin∠CBD=
∠C=90°BD=6∴sin∠CBD=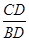 =
=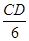 =
=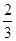 ∴CD="4" 又AD=
∴CD="4" 又AD=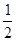 CD∴AD="2" 在Rt△BCD中由勾股定理得;BC2=BD2-CD2即BC2=62-42=20∴BC=
CD∴AD="2" 在Rt△BCD中由勾股定理得;BC2=BD2-CD2即BC2=62-42=20∴BC=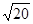 =2
=2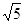 , ∴tanA=
, ∴tanA=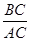 =
=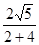 =
=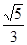
解:在Rt△DBC中,∠C=90,sin∠CBD=
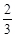 ,DB=6,(如图)
,DB=6,(如图)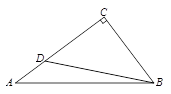
∴
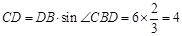 . ……………1分
. ……………1分∴
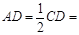
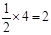 . ………………………2分
. ………………………2分∵
 , 3分
, 3分AC= AD+CD=2+4=6, 4分
在Rt△ABC中,∠C=90,
∴
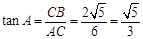 . 5分
. 5分点评:熟知三家函数的定义,正弦等于对边比斜边,正切等于对边比邻边。有一点的难度,但不大。属于基础题。

练习册系列答案
相关题目
 测得楼顶B的仰角α为60°.求楼房BE的高度.(精确到0.1米).
测得楼顶B的仰角α为60°.求楼房BE的高度.(精确到0.1米).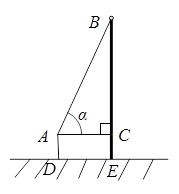
 AB="CD," 对角线
AB="CD," 对角线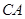 平分
平分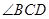 ,AD=5,
,AD=5,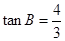 .求:BC的长.
.求:BC的长.
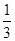 ,BC=
,BC=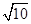 .求AB的长.
.求AB的长. 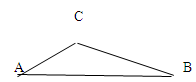
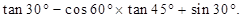
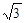 ,2.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有 ( )
,2.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有 ( )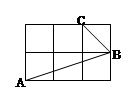
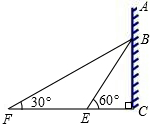
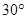 ,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为
,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为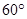 ,求宣传条幅BC的长(小明的身高不计)。
,求宣传条幅BC的长(小明的身高不计)。