题目内容
 如图,AD=CB,∠B=∠D,求证:AB=CD.
如图,AD=CB,∠B=∠D,求证:AB=CD.考点:全等三角形的判定与性质
专题:证明题
分析:延长BA、DC交于O,根据AAS证△OBC≌△ODA,推出OB=OD,OA=OC,即可得出答案.
解答:证明:
延长BA、DC交于O,
在△OBC和△ODA中,
,
∴△OBC≌△ODA(AAS),
∴OB=OD,OA=OC,
∴OB-OA=OD-OC,
∴AB=CD.

延长BA、DC交于O,
在△OBC和△ODA中,
|
∴△OBC≌△ODA(AAS),
∴OB=OD,OA=OC,
∴OB-OA=OD-OC,
∴AB=CD.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 在矩形ABCD中,已知AB=2cm,BC=3cm,现有一根长为2cm的木棒EF紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒EF的中点P在运动过程中所围成的图形的面积为( )
在矩形ABCD中,已知AB=2cm,BC=3cm,现有一根长为2cm的木棒EF紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒EF的中点P在运动过程中所围成的图形的面积为( )| A、6cm2 |
| B、3cm2 |
| C、(2+π)cm2 |
| D、(6-π)cm2 |
点A为数轴上表示-2的点,将点A向左移4个单位长度到B,点B表示的数是( )
| A、2 | B、-6 |
| C、2或-6 | D、以上都不对 |
 将两根木棒AB(长10m),CD(长6m)分别斜立在墙上,其中BE=6m,DE=2m,你能判断哪根更陡吗?请说明理由.
将两根木棒AB(长10m),CD(长6m)分别斜立在墙上,其中BE=6m,DE=2m,你能判断哪根更陡吗?请说明理由. 已知∠AOB,用直尺和圆规作图:
已知∠AOB,用直尺和圆规作图: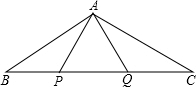 如图,P、Q是△ABC边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC=
如图,P、Q是△ABC边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC= 如图:若B,E,C,F在同一条直线上,AB=DF,AC=DE,BE=CF.求证:∠A=∠D.
如图:若B,E,C,F在同一条直线上,AB=DF,AC=DE,BE=CF.求证:∠A=∠D.