题目内容
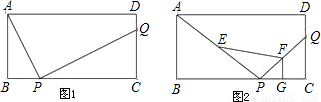
 如图,BP:PQ:QC=1:2:1,CG:AG=1:2,则BE:EF:FG=
如图,BP:PQ:QC=1:2:1,CG:AG=1:2,则BE:EF:FG=
- A.12:17:7
- B.11:16:6
- C.10:15:6
- D.9:14:5
B
分析:可先假设三角形的面积,进而由割补法得出各个小三角形的面积,再由面积与边长之间的关系,进而可得出结论.
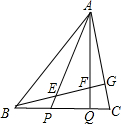
解答: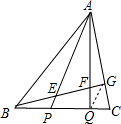 解:连接GQ,由题干的比例关系可得GQ∥AP,
解:连接GQ,由题干的比例关系可得GQ∥AP,
设S△ABC=108,则按面积割补法知:
S△AQC=27,S△GQC=9,GQ∥AP;
S△BGC=36,S△BGQ=27,
S△BFP=3,S△ABP=27,S△ABE=24,
设S△FGQ=x,则S△AFG=18-x,S△ABF=54+x,S△BFQ=27-x,
而S△ABF:S△AFG=BF:FG=S△BFQ:S△FGQ,即(54+x):(18-x)=(27-x):x,
(18-x)(27-x)=x(54-x),化简得99x=486,x=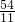 .
.
从而S△AEF=S△ABF-S△ABE=(54+x)-24=30+x=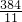 ,S△AFG=18-x=18-
,S△AFG=18-x=18-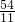 =
=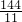 ,
,
则S△ABE:S△AEF:S△AFG=BE:EF:FG=24: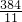 :
: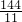 =11:16:6.
=11:16:6.
故选B.
点评:本题主要考查了三角形的面积计算,能够熟练掌握.
分析:可先假设三角形的面积,进而由割补法得出各个小三角形的面积,再由面积与边长之间的关系,进而可得出结论.
解答:
 解:连接GQ,由题干的比例关系可得GQ∥AP,
解:连接GQ,由题干的比例关系可得GQ∥AP,设S△ABC=108,则按面积割补法知:
S△AQC=27,S△GQC=9,GQ∥AP;
S△BGC=36,S△BGQ=27,
S△BFP=3,S△ABP=27,S△ABE=24,
设S△FGQ=x,则S△AFG=18-x,S△ABF=54+x,S△BFQ=27-x,
而S△ABF:S△AFG=BF:FG=S△BFQ:S△FGQ,即(54+x):(18-x)=(27-x):x,
(18-x)(27-x)=x(54-x),化简得99x=486,x=
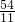 .
.从而S△AEF=S△ABF-S△ABE=(54+x)-24=30+x=
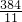 ,S△AFG=18-x=18-
,S△AFG=18-x=18-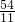 =
=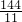 ,
,则S△ABE:S△AEF:S△AFG=BE:EF:FG=24:
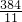 :
: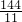 =11:16:6.
=11:16:6.故选B.
点评:本题主要考查了三角形的面积计算,能够熟练掌握.

练习册系列答案
相关题目
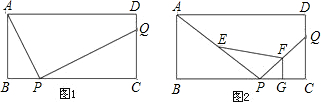 的中点,求四边形EPGF的面积.
的中点,求四边形EPGF的面积.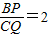 ,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.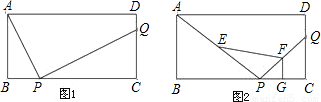
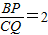 ,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.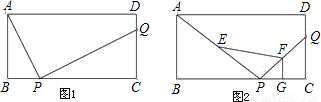
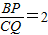 ,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.