题目内容
已知:如图①,②,在矩形ABCD中,AB=4,BC=8,P,Q分别是边BC,CD上的点.(1)如图①,若AP⊥PQ,BP=2,求CQ的长;
(2)如图②,若
| BP | CQ |
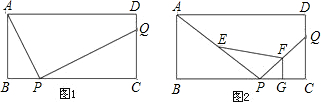 的中点,求四边形EPGF的面积.
的中点,求四边形EPGF的面积.
分析:(1)、由同角的余角相等可得∠APB=∠PQC,故△ABP∽△PCQ,有
=
,代入BP,AB,PC的值求得CQ的值;
(2)、取BP的中点H,连接EH,由三角形的中位线的性质可得四边形EHGF是直角梯形,由
=2,设CQ=a,有BP=2a,用含a的代数式表示出EH,FG,HP,HG,两用梯形和三角形的面积公式求得S四边形EPGF=S梯形EHGF-S△EHP的值.
| BP |
| AB |
| CQ |
| PC |
(2)、取BP的中点H,连接EH,由三角形的中位线的性质可得四边形EHGF是直角梯形,由
| BP |
| CQ |
解答: 解:(1)∵四边形ABCD是矩形
解:(1)∵四边形ABCD是矩形
∴∠B=∠C=90°,
∴∠CPQ+∠PQC=90°,
∵AP⊥PQ,
∴∠CPQ+∠APB=90°,
∴∠APB=∠PQC,
∴△ABP∽△PCQ,
∴
=
,即
=
,
∴CQ=3;
(2)解法一:取BP的中点H,连接EH,由
=2,
设CQ=a,则BP=2a,
∵E,F,G,H分别为AP,PQ,PC,BP的中点,
∴EH∥AB,FG∥CD,
又∵AB∥CD,∠B=∠C=90°,
∴EH∥FG,EH⊥BC,FG⊥BC,
∴四边形EHGF是直角梯形,
∴EH=
AB=2,FG=
CQ=
a,HP=
BP=a,HG=HP+PG=
BC=4,
∴S梯形EHGF=
(EH+FG)•HG=
(2+
a)•4=4+a,S△EHP=
HP•EH=
a•2=a,
∴S四边形EPGF=S梯形EHGF-S△EHP=4+a-a=4;
解法二:连接AQ,由
=2,设CQ=a,则BP=2a,DQ=4-a,PC=8-2a,S△APQ=S矩形ABCD-S△ABP-S△PCQ-S△ADQ
=4×8-
•2a•4-
(8-2a)a-
×8(4-a)
=a2-4a+16
∵E,F,G分别是AP,PQ,PC的中点
∴EF∥AQ,EF=
AQ.∴△PEF∽△PAQ
∴
=
,S△PEF=
S△APQ=
(a2-4a+16)
同理:S△PFG=
S△PCQ=
a(8-2a)
∴S四边形EPGF=S△PEF+S△PFG
=
(a2-4a+16)+
a(8-2a)=4.
 解:(1)∵四边形ABCD是矩形
解:(1)∵四边形ABCD是矩形∴∠B=∠C=90°,
∴∠CPQ+∠PQC=90°,
∵AP⊥PQ,
∴∠CPQ+∠APB=90°,
∴∠APB=∠PQC,
∴△ABP∽△PCQ,
∴
| BP |
| AB |
| CQ |
| PC |
| 2 |
| 4 |
| CQ |
| 8-2 |
∴CQ=3;
(2)解法一:取BP的中点H,连接EH,由
| BP |
| CQ |
设CQ=a,则BP=2a,
∵E,F,G,H分别为AP,PQ,PC,BP的中点,
∴EH∥AB,FG∥CD,
又∵AB∥CD,∠B=∠C=90°,
∴EH∥FG,EH⊥BC,FG⊥BC,
∴四边形EHGF是直角梯形,
∴EH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S梯形EHGF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形EPGF=S梯形EHGF-S△EHP=4+a-a=4;
解法二:连接AQ,由
| BP |
| CQ |
=4×8-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=a2-4a+16
∵E,F,G分别是AP,PQ,PC的中点
∴EF∥AQ,EF=
| 1 |
| 2 |
∴
| S△PEF |
| S△APQ |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
同理:S△PFG=
| 1 |
| 4 |
| 1 |
| 8 |
∴S四边形EPGF=S△PEF+S△PFG
=
| 1 |
| 4 |
| 1 |
| 8 |
点评:本题利用了矩形的性质,相似三角形的判定和性质,三角形和梯形的面积公式求解.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
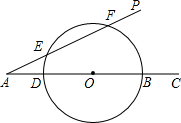 已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.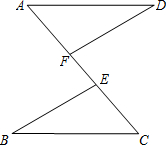 13、已知:如图,E、F在AC上,AD∥CB且AD=CB,∠D=∠B.
13、已知:如图,E、F在AC上,AD∥CB且AD=CB,∠D=∠B.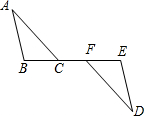 已知:如图,C、F在BE上,∠A=∠D,AB∥DE,AB=DE.
已知:如图,C、F在BE上,∠A=∠D,AB∥DE,AB=DE. 22、已知:如图,D、E在BC上,AB=AC,AD=AE.试说明线段BD与CE相等的理由.
22、已知:如图,D、E在BC上,AB=AC,AD=AE.试说明线段BD与CE相等的理由.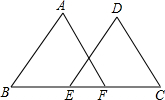 已知:如图,E、F两点在BC上,BE=CF,AB∥DE,AF∥CD
已知:如图,E、F两点在BC上,BE=CF,AB∥DE,AF∥CD