题目内容
如图,在正方形ABCD中,E为AB的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
A. | B.2 | C. | D.3 |
D.
解析试题分析:∵四边形ABCD是正方形,∴∠A=∠B=90°,∴∠AGE+∠AEG=90°,∵∠GEF=90°,∴∠AEG+∠BEF=90°,∴∠AGE=∠BEF,∴△AGE∽△BEF,∴ ,∵E为AB的中点,∴AE=BE,∵AG=1,BF=2,∴
,∵E为AB的中点,∴AE=BE,∵AG=1,BF=2,∴ ,解得:BE=AE=
,解得:BE=AE= ,在Rt△AEG中,GE2=AG2+AE2=3,在Rt△BEF中,EF2=BE2+BF2=6,∴在Rt△GEF中,GF=
,在Rt△AEG中,GE2=AG2+AE2=3,在Rt△BEF中,EF2=BE2+BF2=6,∴在Rt△GEF中,GF= =3.故选D.
=3.故选D.
考点:1.相似三角形的判定与性质;2.勾股定理;3.正方形的性质.

练习册系列答案
相关题目
如图,在 中,DE∥BC,且AD:AB=2:3,则DE:BC的值为
中,DE∥BC,且AD:AB=2:3,则DE:BC的值为
A. | B. | C. | D.2 |
如果 ,那么下列比例式变形正确的是
,那么下列比例式变形正确的是
A. | B. | C. | D. |
如图,在△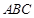 中,点
中,点 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且 ∥
∥ ,若
,若 ,
,  ,
, 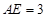 ,则
,则 的长为( )
的长为( )
| A.3 | B.6 | C.9 | D.12 |
已知△ABC和△DEF相似,且△ABC的三边长为3、4、5,如果△DEF的周长为6,那么下列不可能是△DEF一边长的是( )
| A.1.5; | B.2; | C.2.5; | D.3. |
下列四组图形中,一定相似的是
| A.正方形与矩形 | B.正方形与菱形 |
| C.菱形与菱形 | D.正五边形与正五边形 |