题目内容
解方程:
+
+…+
=2013.
| x |
| 1×2 |
| x |
| 2×3 |
| x |
| 2013×2014 |
考点:解一元一次方程
专题:
分析:根据
+
+…+
=(1-
)+(
-
)+…+(
-
)的规律来解方程.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2013×2014 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
解答:解:∵
+
+…+
=(1-
)+(
-
)+…+(
-
)
=1-
+
-
+…+
-
=1-
=
,
∴x(
+
+…+
)=x(1-
)+(
-
)+…+(
-
)=
x=2013,
解得 x=2014.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2013×2014 |
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
=1-
| 1 |
| 2014 |
=
| 2013 |
| 2014 |
∴x(
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2013×2014 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
解得 x=2014.
点评:本题考查了解一元一次方程.解题的关键是把原方程转化为一元一次方程的一般形式.

练习册系列答案
相关题目
把抛物线y=-5x2向左平移2个单位,再向下平移3个单位,得到抛物线是( )
| A、y=-5(x+2)2+3 |
| B、y=-5(x+2)2-3 |
| C、y=-5(x-2)2+3 |
| D、y=-5(x-2)2-3 |
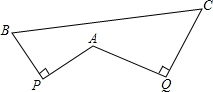 如图,PA=PB且PA⊥PB,QA=QC且QA⊥QC.
如图,PA=PB且PA⊥PB,QA=QC且QA⊥QC. 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.