题目内容
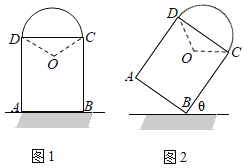
【题目】由四个正方形相框拼成的照片墙如图所示,已知正方形![]() ,正方形
,正方形![]() ,正方形
,正方形![]() 的.面积分别为
的.面积分别为![]() 平方分米,
平方分米,![]() 平方分米,
平方分米,![]() 平方分米,则正方形
平方分米,则正方形![]() 的面积为__________平方分米.
的面积为__________平方分米.
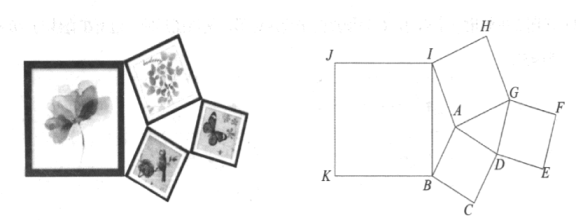
【答案】6
【解析】
作出如图的辅助线,证得![]() ,继而推出
,继而推出![]() ,在Rt△IBQ和Rt△ABQ中,设参数利用勾股定理即可求解.
,在Rt△IBQ和Rt△ABQ中,设参数利用勾股定理即可求解.
如图:作AM⊥BI于M,延长MA交DG于N,分别过D、G作MN的垂线垂足分别为R、S,

∴∠RDN=∠SGN,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90![]() ,
,
∴∠MBA+∠MAB=90![]() ,∠RAD+∠MAB=90
,∠RAD+∠MAB=90![]() ,
,
∴∠MBA=∠RAD,
在Rt△MBA和Rt△RAD中,
 ,
,
∴Rt△MBA![]() Rt△RAD,
Rt△RAD,
∴AM=DR,
同理可证得,Rt△MIA![]() Rt△SAG,
Rt△SAG,
∴AM=GS,
∴DR=GS,
在Rt△RDN和Rt△SGN中,
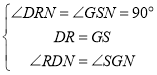 ,
,
∴Rt△RDN![]() Rt△SGN,
Rt△SGN,
∴![]() ;
;
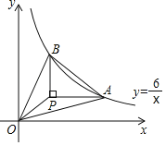
作DP⊥AG于P,作BQ⊥IA交IA延长线于Q,如图:

∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在Rt△ABQ和Rt△ADP中,
![]() ,AB=AD,
,AB=AD,
∴Rt△ABQ![]() Rt△ADP(HL),
Rt△ADP(HL),
∴AQ =AP,
设正方形AGHI的边长为![]() ,
,
由题意,![]() ,DA=DG=
,DA=DG=![]() ,
,![]() ,AP=PG=
,AP=PG=![]() ,AQ =AP
,AQ =AP![]() ,
,
在Rt△IBQ和Rt△ABQ中,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴正方形AGHI的面积为:![]() .
.
故答案为:![]() .
.

【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.