Question

【题目】如图，在中，，，．点从点开始沿边向点以的速度移动，与此同时，点从点开始沿边向点以的速度移动．设、分别从、同时出发，运动时间为，当其中一点先到达终点时，另一点也停止运动．解答下列问题：

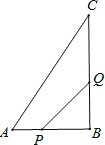
（1）经过几秒，的面积等于？

（2）是否存在这样的时刻，使线段恰好平分的面积？若存在，求出运动时间；若不存在，请说明理由．

Answer 1

【答案】（1）2秒；（2）不存在

【解析】

（1）设出运动所求的时间，可将BP和BQ的长表示出来，代入三角形面积公式，列出等式，可将时间求出；

（2）将△PBQ的面积表示出来，根据△=b2-4ac来判断．

（1）设经过秒，的面积等于则：

，，

所以，即，

可得：或4（舍去），

即经过2秒，的面积等于．

（2）设经过秒，线段恰好平分的面积，的面积等于，，

即，

因为△，所以的面积不会等于，则线段不能平分的面积．