题目内容
如图,矩形ABCD中,以对角线BD为一边构成一个矩形BDEF,使得另一边EF过原矩形的顶点C
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1 S2+S3(用“>”、“=”、“<”填空);
(2)写出如图中的三对相似三角形,并选择其中一对进行证明.
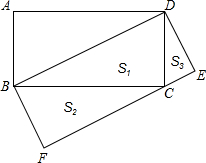
(1)解:∵S1= BD×ED,S矩形BDEF=BD×ED,
BD×ED,S矩形BDEF=BD×ED,
∴S1= S矩形BDEF,
S矩形BDEF,
∴S2+S3= S矩形BDEF,
S矩形BDEF,
∴S1=S2+S3.
(2)答:△BCD∽△CFB∽△DEC.
证明△BCD∽△DEC;
证明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,
∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,
∴△BCD∽△DEC.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
浙江省居民生活用电可申请峰谷电,峰谷电价如下表:
| 高峰时间段用电价格表 | 低谷时间段用电价格表 | |
| 高峰电价 (单位:元/千瓦时) | 低谷月用电量 (单位:千瓦时) | 低谷电价 (单位:元/千瓦时) |
| 0.568 | 50及以下的部分 | 0.288 |
| 超过50至200的部分 | 0.318 | |
| 超过200的部分 | 0.388 |
小远家5月份的高峰时间用电量为200千瓦时,低谷时间段用电量为300千瓦时,则按这种计费方式该家庭本月应付的电费为________元(精确到角).
由一些大小相同的小正方体搭成的几何体的主视图和左视图如图,则搭成该几何体的小正方体的个数最少是( )

|
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |

 的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的
的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的

 ① =90°; ② DO∥AB; ③ CD=AD; ④△BDE∽△BCD; ⑤
① =90°; ② DO∥AB; ③ CD=AD; ④△BDE∽△BCD; ⑤

 ﹣1)0﹣
﹣1)0﹣ .
.