题目内容
【题目】如图,等边三角形![]() 的边长为4,
的边长为4,![]() 为边
为边![]() 上一点,过点
上一点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,在
,在![]() 右侧作等边三角形
右侧作等边三角形![]() ,记
,记![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到
到![]() 的距离为
的距离为![]() ,
,
(1)若![]() ,试求线段
,试求线段![]() 的长,并求m1、m2的值.
的长,并求m1、m2的值.
(2)若![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ,
,![]() ,并求
,并求![]() 在∠C的平分线上时x的值.
在∠C的平分线上时x的值.

【答案】(1)DE=![]() ,m1=
,m1=![]() ,m2=0;(2)
,m2=0;(2)![]() ,
,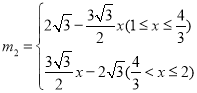 ,当
,当![]() 在
在![]() 的平分线上时x=1.
的平分线上时x=1.
【解析】
(1)过点![]() 作
作![]() ,则
,则![]() ,延长DP交AC于点G,由题意可得:△BED、△DFP、DGC、均为30°的直角三角形,由
,延长DP交AC于点G,由题意可得:△BED、△DFP、DGC、均为30°的直角三角形,由![]() 可得
可得![]() ,由等边三角形
,由等边三角形![]() 可得
可得![]() ,故
,故![]() 由于
由于![]() ,可得
,可得![]() 故
故![]() ;
;
(2)由(1)得当点P在三角形ABC内部时,![]() ;
;
①当![]() 时,点P在三角形ABC内部, 此时,同(1)中的思路;②当
时,点P在三角形ABC内部, 此时,同(1)中的思路;②当![]() 时,点P在三角形ABC一边上,同(1)可知
时,点P在三角形ABC一边上,同(1)可知![]() ,
,![]() ,
,
③当![]() 时,点P在三角形ABC外部时,过点
时,点P在三角形ABC外部时,过点![]() 做
做![]() ,则
,则![]() , DP与AC交于点G. 由题意可得:△BED、△DFP、DGC、均为30°的直角三角形可得
, DP与AC交于点G. 由题意可得:△BED、△DFP、DGC、均为30°的直角三角形可得![]() ,由等边三角形
,由等边三角形![]() 可得
可得![]() ,故
,故![]() ,
,
由DC=BC-BD=4-x可得![]() ,故
,故![]() ;当
;当![]() 在
在![]() 的平分线上时,此时
的平分线上时,此时![]() 在三角形内部
在三角形内部![]() ,有
,有![]() 列出方程
列出方程 ![]() 求解即可;
求解即可;
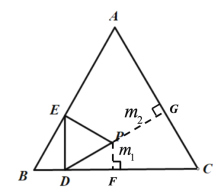
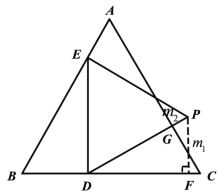
解:(1)如下图,过点![]() 作
作![]() ,则
,则![]() ,延长DP交AC于点G.
,延长DP交AC于点G.
![]()
∵DE⊥BC,∠EDP=60°,
∴∠PDC=30°,
∵∠C=60°,
∴∠DGC=180°-∠PDC-∠C=90°,
∴![]() ,
,
∵![]() ,∠B=60°,∠BDE=90°,
,∠B=60°,∠BDE=90°,
∴![]() ,
,
∵![]() ,∠PDC=30°,PF⊥BC,
,∠PDC=30°,PF⊥BC,
∴![]() ,
,
∵![]() ,
,
且∠C=60°,PG⊥AC,
∴![]() ,
,
∴![]() ;
;
(2)由(1)得当点P在三角形ABC内部时,![]() ,
,
①当![]() 时,点P在三角形ABC内部,同(1)如下图,
时,点P在三角形ABC内部,同(1)如下图,

同(1)可证∠DGC=90°,
∴![]() ,
,
∵![]() ,∠B=60°,∠BDE=90°,
,∠B=60°,∠BDE=90°,
∴![]() ,
,
∵![]() ,∠PDC=30°,PF⊥BC,
,∠PDC=30°,PF⊥BC,
∴![]() ,
,
∵DC=BC-BD=4-x,
且∠C=60°,PG⊥AC,
∴![]() ,
,
∴![]() ,
,
②当![]() 时,点P在三角形ABC一边上,
时,点P在三角形ABC一边上,
同(1)可知![]() ,
,![]() ,
,
③当![]() 时,点P在三角形ABC外部,
时,点P在三角形ABC外部,
如下图,过点![]() 做
做![]() ,则
,则![]() , DP与AC交于点G.
, DP与AC交于点G.
同(1)可证∠DGC=90°,
∴![]() ,
,
∵BD=x,∠B=60°,∠BDE=90°,
∴![]() ,
,
∵![]() ,∠PDC=30°,PF⊥BC,
,∠PDC=30°,PF⊥BC,
∴![]() ,
,
∵DC=BC-BD=4-x,
且∠C=60°,PG⊥AC,
∴![]() ,
,
∴![]() ,
,
综上所述, ,
,
当![]() 在
在![]() 的平分线上时,易知
的平分线上时,易知![]() 在三角形内部
在三角形内部![]() ,有
,有![]() ,
,
即 ![]() ,
,
解得 x=1;

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案