题目内容
正方形ABCD的对角线AC、BD相交于点O，E是BC中点，DE交AC于F，若DE=12，则EF等于（ ）A．8
B．6
C．4
D．3
【答案】分析：先根据题意画出图形，因为四边形ABCD是正方形，E是BC中点，所以CE=
AD，由相似三角形的判定定理得出△CEF∽△ADF，再根据相似三角形的对应边成比例可得出
=
=
，再根据DF=DE-EF即可得出EF的长．
解答：
解：如图所示：
∵四边形ABCD是正方形，E是BC中点，
∴CE=
AD，
∵AD∥BC，
∴∠ADF=∠DEC，∠AFD=∠EFC，
∴△CEF∽△ADF，
∴
=
=
，
=
，即
=
，
解得EF=4．
故选C．
点评：本题考查的是相似三角形的判定与性质及正方形的性质，先根据题意判断出△CEF∽△ADF，再根据相似三角形的对应边成比例进行解答是解答此题的关键．
AD，由相似三角形的判定定理得出△CEF∽△ADF，再根据相似三角形的对应边成比例可得出==，再根据DF=DE-EF即可得出EF的长．解答：
解：如图所示：∵四边形ABCD是正方形，E是BC中点，
∴CE=
AD，∵AD∥BC，
∴∠ADF=∠DEC，∠AFD=∠EFC，
∴△CEF∽△ADF，
∴
==，=，即=，解得EF=4．
故选C．
点评：本题考查的是相似三角形的判定与性质及正方形的性质，先根据题意判断出△CEF∽△ADF，再根据相似三角形的对应边成比例进行解答是解答此题的关键．
练习册系列答案
相关题目
8、如图，正方形ABCD的对角AC，BD交于点O，，则结论①AB=BC=CD=DA；②AO=BO=CO=DO；③AC⊥BD中正确的有（ ）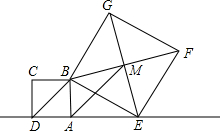
如图，已知正方形ABCD的边长为1，点E是射线DA一动点（DE＞1），连结BE，以BE为边在BE上方作正方形BEFG，设M为正方形BEFG的中心，如果定义：只有一组对角是直角的四边形叫做损矩形．
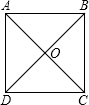如图，正方形ABCD的对角AC，BD交于点O，则结论①AB=BC=CD=DA；②AO=BO=CO=DO；③AC⊥BD中正确的有
