Question

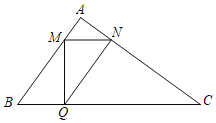
【题目】如图，在ABC中，∠A＝90°，AB＝3，AC＝4，点M、Q分别是边AB、BC上的动点（点M不与A、B重合），且MQ⊥BC，过点M作MN∥BC．交AC于点N，连接NQ，设BQ＝x．

（1）是否存在一点Q，使得四边形BMNQ为平行四边形，并说明理由；

（2）当BM＝2时，求x的值；

（3）当x为何值时，四边形BMNQ的面积最大，并求出最大值．

Answer 1

【答案】（1）存在，当BQ＝MN=时，四边形BMNQ为平行四边形，见解析；（2）；（3）当x＝时，四边形BMNQ的面积最大，最大值为

【解析】

（1）先证明△AMN∽△ABC，得到＝＝；再设AM＝3a、则MN＝5a，即BQ＝MN＝5a．然后再证明△MBQ∽△NMA，再运用相似三角形的性质列式求出a，进而求得BQ的长；再由MN∥BQ，即可得到BQ＝MN＝，四边形BMNQ为平行四边形；

（2）再证△BMQ∽△BCA可得＝，即＝，最后求解即可；

（3）先由勾股定理求出BC的长，再根据相似三角形的性质用x表示出QM、BM，然后根据梯形面积公式列出二次函数解析式，最后根据二次函数性质计算即可．

解：（1）存在，理由如下：

∵MN∥BC，

∴△AMN∽△ABC，

∴＝＝，

设AM＝3a，则MN＝5a，

∴BQ＝MN＝5a，

∵MN∥BQ，

∴∠NMQ＝∠MQB＝90°，

∴∠AMN+∠BMQ＝90°，

又∠B+∠BMQ＝90°，

∴∠B＝∠AMN，

又∠MQB＝∠A＝90°，

∴△MBQ∽△NMA，

∴＝，即＝，

解得a＝，

∴BQ＝，

∵MN∥BQ，

∴当BQ＝MN＝，四边形BMNQ为平行四边形；

∴当BQ＝MN时，四边形BMNQ为平行四边形，

（2）∵∠BQM＝∠A＝90°，∠B＝∠B，

∴△BMQ∽△BCA，

∴＝，即＝，

解得x＝；

（3）∵∠A＝90°，AB＝3，AC＝4，

∴BC＝＝5，

∵△QBM∽△ABC，

∴＝＝，即＝＝，

解得，QM＝x，BM＝x，

∵MN∥BC，

∴＝，即＝，

解得，MN＝5﹣x，则四边形BMNQ的面积＝×（5﹣x+x）×x＝﹣（x﹣）2+，

∴当x＝时，四边形BMNQ的面积最大，最大值为．