题目内容
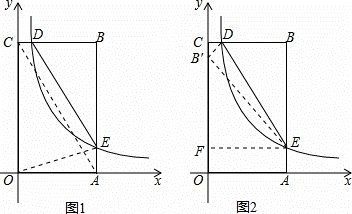
如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=  (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.
(1)连接OE,若△EOA的面积为2,则k= ;
(2)连接CA,请问DE与CA是否平行?请说明理由;
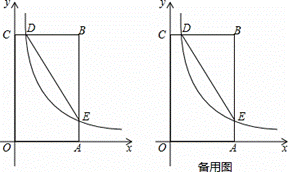 (3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
解:(1)连接OE,如,图1,
∵Rt△AOE的面积为2, ∴k=2×2=4.………………3分
(2)连接AC,如图1,设D(x,5),E(3,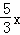 ),则BD=3﹣x,BE=5﹣
),则BD=3﹣x,BE=5﹣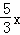 ,
,
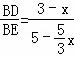 =
=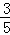 ,
,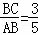
∴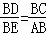 ∴DE∥AC.………………6分
∴DE∥AC.………………6分
(3)假设存在点D满足条件.设D(x,5),E(3,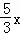 ),则CD=x,
),则CD=x,
BD=3﹣x,BE=5﹣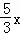 ,AE=
,AE=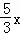 .
.
作EF⊥OC,垂足为F,如图2,
易证△B′CD∽△EFB′,
∴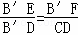 ,即
,即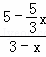 =
=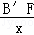 ,
,
∴B′F=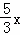 ,
,
∴OB′=B′F+OF=B′F+AE=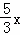 +
+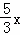 =
=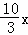 ,
,
∴CB′=OC﹣OB′=5﹣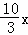 ,
,
在Rt△B′CD中,CB′=5﹣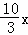 ,CD=x,B′D=BD=3﹣x,
,CD=x,B′D=BD=3﹣x,
由勾股定理得,CB′2+CD2=B′D2,
(5﹣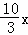 )2+x2=(3﹣x)2,
)2+x2=(3﹣x)2,
解这个方程得,x1=1.5(舍去),x2=0.96,
∴满足条件的点D存在,D的坐标为D(0.96,5).………………10分

从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
| 种子粒数 | 100 | 400 | 800 | 1 000 | 2 000 | 5 000 |
| 发芽种子粒数 | 85 | 398 | 652 | 793 | 1 604 | 4 005 |
| 发芽频率 | 0.850 | 0.745] | 0.851 | 0.793 | 0.802 | 0.801 |
根据以上数据可以估计,该玉米种子发芽的概率约为 (精 确到0.1).
确到0.1).
 。
。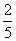 ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况; 好;C级:及格;D级:不及格),并将测试结果绘成了
好;C级:及格;D级:不及格),并将测试结果绘成了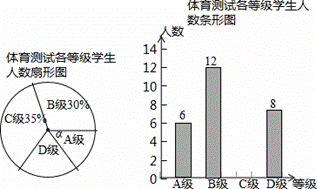 (2)图1中∠α的度数是 ,并把图2条形统计图补充完整;
(2)图1中∠α的度数是 ,并把图2条形统计图补充完整; B.
B. 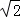 ﹣1 C. 2﹣
﹣1 C. 2﹣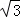 D.
D. 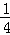
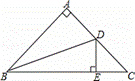
 ,则CQ最大值为( )
,则CQ最大值为( ) C.
C.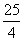 D.
D.
 化为
化为 的形式,结果为( )
的形式,结果为( ) B.
B.
 D.
D.
 ,
, =8,且
=8,且 <0,则
<0,则 的值等于 ( )
的值等于 ( ) B.
B. C.
C. 或11 D.
或11 D.