Question

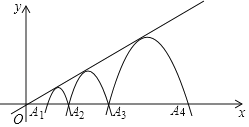
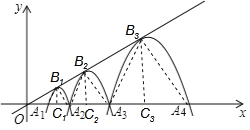
【题目】若二次函数的图象与x轴的两个交点和顶点构成等边三角形，则称这样的二次函数的图象为标准抛物线．如图，自左至右的一组二次函数的图象T1，T2，T3……是标准抛物线，且顶点都在直线y=x上，T1与x轴交于点A1(2，0)，A2(A2在A1右侧)，T2与x轴交于点A2，A3，T3与x轴交于点A3，A4，……，则抛物线Tn的函数表达式为_____．

Answer 1

【答案】

【解析】

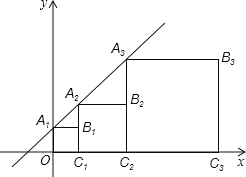
设抛物线T1，T2，T3…的顶点依次为B1，B2，B3…，连接A1B1，A2B1，A2B2，A3B2，A3B3，A4B3…，过抛物线各顶点作x轴的垂线，由△A1B1A2是等边三角形，结合顶点都在直线y=x上，可以求出，A2(4，0)，进而得到T1的表达式：，同理，依次类推即可得到结果．

解：设抛物线T1，T2，T3…的顶点依次为B1，B2，B3…，连接A1B1，A2B1，A2B2，A3B2，A3B3，A4B3…，过抛物线各顶点作x轴的垂线，如图所示：

∵△A1B1A2是等边三角形，

∴∠B1A1A2=60°，

∵顶点都在直线y=x上，设，

∴OC1=m，，

∴，

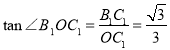∴∠B1OC1=30°，

∴∠OB1A1=30°，

∴OA1=A1B1=2=A2B1，

∴A1C1=A1B1cos60°=1，

，

∴OC1=OA1+A1C1=3，

∴，A2(4，0)，

设T1的解析式为：，

则，

∴，

∴T1：，

同理，T2的解析式为：，

T3的解析式为：，

…

则Tn的解析式为：，

故答案为：．