题目内容
 如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若AC=8,AB=12,BO=13,求:
如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若AC=8,AB=12,BO=13,求:
(1)⊙O的半径;
(2)把 沿弦AC向上翻转180°,问翻转后的
沿弦AC向上翻转180°,问翻转后的 是否经过圆心O,并说明理由.
是否经过圆心O,并说明理由.
解:(1)∵AB是⊙O的切线,A为切点,
∴∠BAO=90°,
∵AB=12,BO=13,
∴OA=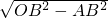 =
= =5;
=5;
(2)不经过,
∵AH=8÷2=4,
∴OH= =3,
=3,
∵3×2>5,
∴翻转后的 不经过圆心O.
不经过圆心O.
分析:(1)要求⊙O的半径,可找半径OA所在的△OAB;因为AB是⊙O的切线,A为切点,得出∠BAO=90°,在△OAB中应用勾股定理求出⊙O的半径;
(2)翻转180°对应点到对称轴的距离相等,可以在△OHA中应用勾股定理求出OH的长,它的两倍与半径长比较.
点评:此题主要考查切线的性质及直角三角形的勾股定理.
∴∠BAO=90°,
∵AB=12,BO=13,
∴OA=
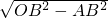 =
= =5;
=5;(2)不经过,
∵AH=8÷2=4,
∴OH=
 =3,
=3,∵3×2>5,
∴翻转后的
 不经过圆心O.
不经过圆心O.分析:(1)要求⊙O的半径,可找半径OA所在的△OAB;因为AB是⊙O的切线,A为切点,得出∠BAO=90°,在△OAB中应用勾股定理求出⊙O的半径;
(2)翻转180°对应点到对称轴的距离相等,可以在△OHA中应用勾股定理求出OH的长,它的两倍与半径长比较.
点评:此题主要考查切线的性质及直角三角形的勾股定理.

练习册系列答案
相关题目
 12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD=
12、已知,如图,AB是⊙O的直径,DC切⊙O于点C,AB=2BC,则∠BCD= 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )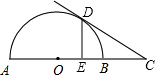
 21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD.
21、如图,AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.求证:AC平分∠BAD. 如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为
如图,AB是半圆的直径,直线MN切半圆于点C,AM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的直径为