题目内容
在⊙O中,已知⊙O的直径AB为2,弦AC的长为 ,弦AD的长为
,弦AD的长为 ,则DC2=________.
,则DC2=________.
2+ 或 2-
或 2-
分析:根据垂径定理和勾股定理可得.
解答: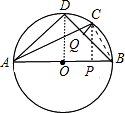 解:连接AD,AC,BC,BD,
解:连接AD,AC,BC,BD,
∵直径AB=2,弦AC= ,弦AD=
,弦AD=
∴BC2=(AB2-AC2)=22-( )2=1,
)2=1,
BD2=(AB2-AD2)=22-( )2=2,
)2=2,
∴BC=1,BD=
∴∠ABC=60°,∠ABD=45°,
过点C作CP⊥AB交于点P,作CQ⊥DQ交于点Q,
则BP= BC=
BC= ,OQ=OC-CQ=CP=
,OQ=OC-CQ=CP= ,OP=OB-BP=
,OP=OB-BP= ,
,
如果弦AC,AD在同一个半圆,
则DQ=OD-OQ=1- =
=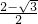
∴CD2=DQ2+QC2=DQ2+OP2=(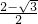 )2+(
)2+( )2=2-
)2=2- .
.
如果弦AC,AD分别在两个半圆,
则DQ=OD+OQ=1+ =
=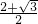
∴CD2=DQ2+QC2=DQ2+OP2=(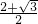 )2+(
)2+( )2=2+
)2=2+ .
.
故答案为 2+ 或 2-
或 2- .
.
点评:此题主要考查了垂径定理和勾股定理.分两种情况讨论是解决此类问题的关键.
 或 2-
或 2-
分析:根据垂径定理和勾股定理可得.
解答:
 解:连接AD,AC,BC,BD,
解:连接AD,AC,BC,BD,∵直径AB=2,弦AC=
 ,弦AD=
,弦AD=
∴BC2=(AB2-AC2)=22-(
 )2=1,
)2=1,BD2=(AB2-AD2)=22-(
 )2=2,
)2=2,∴BC=1,BD=

∴∠ABC=60°,∠ABD=45°,
过点C作CP⊥AB交于点P,作CQ⊥DQ交于点Q,
则BP=
 BC=
BC= ,OQ=OC-CQ=CP=
,OQ=OC-CQ=CP= ,OP=OB-BP=
,OP=OB-BP= ,
,如果弦AC,AD在同一个半圆,
则DQ=OD-OQ=1-
 =
=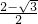
∴CD2=DQ2+QC2=DQ2+OP2=(
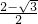 )2+(
)2+( )2=2-
)2=2- .
.如果弦AC,AD分别在两个半圆,
则DQ=OD+OQ=1+
 =
=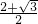
∴CD2=DQ2+QC2=DQ2+OP2=(
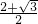 )2+(
)2+( )2=2+
)2=2+ .
.故答案为 2+
 或 2-
或 2- .
.点评:此题主要考查了垂径定理和勾股定理.分两种情况讨论是解决此类问题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 19、如图,在?ABCD中,已知∠BAD的平分线AE交BC于点E,AD=5cm,CE=2cm,则?ABCD的周长为
19、如图,在?ABCD中,已知∠BAD的平分线AE交BC于点E,AD=5cm,CE=2cm,则?ABCD的周长为