题目内容
【题目】 如图,△ABC是 ![]() 的内接等边三角形,AB=1.点D , E在圆上,四边形
的内接等边三角形,AB=1.点D , E在圆上,四边形 ![]() 为矩形,则这个矩形的面积是( )
为矩形,则这个矩形的面积是( )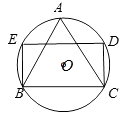
A.![]()
B.![]()
C.![]()
D.1
【答案】A
【解析】过点O作OF⊥BC,连接OC,BD,
∵△ABC是⊙O的内接等边三角形,AB=1,
∴BF=![]() BC=
BC=![]() ,∠OBC=30°,
,∠OBC=30°,
在Rt△OBF中,设OF=x,OB=2x,
∴OB2=OF2+BF2,
即4x2=x2+![]() ,
,
∴OF=x= ![]() ,OB=2x=
,OB=2x=![]() ,
,
∴BD=2OB=![]() ,CD=
,CD=![]() BD=
BD=![]() ,
,
∴SBEDC=BC.CD=1×![]() .
.
所以答案是:A.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对含30度角的直角三角形的理解,了解在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目