题目内容
如图,△ABC的高AD为3,BC为4,直线EF∥BC,交线段AB于E,交线段AC于F,交AD于G,以EF为斜边作等腰直角三角形PEF(点P与点A在直线EF的异侧),设EF为x,△PEF与四边形BCEF重合部分的面积为y.(1)求线段AG(用x表示);
(2)求y与x的函数关系式,并求x的取值范围.

【答案】分析:(1)由图和已知条件知,△AEF∽△ABC从而得AG表达式,分两种情况当点P在四边形BCFE的内部或BC边上时易得PH= x的关系;
x的关系;
(2)当点P在四边形BCFE的外部时,过点P作PH⊥EF易得PH=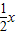 ,从而推出△PMN∽△PEF根据比例关系推出△PMN为等腰三角形,把△PMN用x表示出来,最后根据边长关系求出x的取值范围.
,从而推出△PMN∽△PEF根据比例关系推出△PMN为等腰三角形,把△PMN用x表示出来,最后根据边长关系求出x的取值范围.
解答: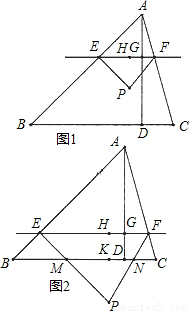 解:(1)∵EF∥BC,
解:(1)∵EF∥BC,
∴△AEF∽△ABC,
∴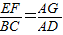 ,
,
∴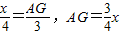 .
.
(2)当点P在四边形BCFE的内部或BC边上时,如图1过点P作PH⊥EF于H,
∵等腰直角三角形PEF,
∴PH=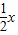 ,
,
∴y=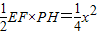 .
.
∵PH≤DG,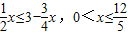 .
.
当点P在四边形BCFE的外部时,如图2,
过点P作PH⊥EF于H,交MN于K,同理得PH=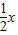 ,
,
∵EF∥BC,
∴∠KHG=∠HKD=90°,
∴四边形HGDK为矩形,
∴HK=DG=3-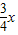 ,
,
∴PK=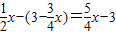 ,
,
∵EF∥BC,
∴△PMN∽△PEF,
∴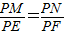 ,
,
∴△PMN为等腰直角三角形.
∴S△PMN= MN×PK=PK2=
MN×PK=PK2=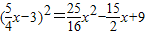 ,
,
∴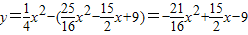 ,
,
∵PH>DG,
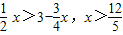
∴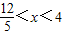 .
.
点评:此题多次用到三角形相似的性质,这也是平面几何题通常用的方法,作辅助线找三角形相似,把几何关系用函数表示出来,并求出定义域,是很好的题型.
 x的关系;
x的关系;(2)当点P在四边形BCFE的外部时,过点P作PH⊥EF易得PH=
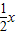 ,从而推出△PMN∽△PEF根据比例关系推出△PMN为等腰三角形,把△PMN用x表示出来,最后根据边长关系求出x的取值范围.
,从而推出△PMN∽△PEF根据比例关系推出△PMN为等腰三角形,把△PMN用x表示出来,最后根据边长关系求出x的取值范围.解答:
 解:(1)∵EF∥BC,
解:(1)∵EF∥BC,∴△AEF∽△ABC,
∴
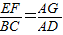 ,
,∴
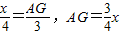 .
.(2)当点P在四边形BCFE的内部或BC边上时,如图1过点P作PH⊥EF于H,
∵等腰直角三角形PEF,
∴PH=
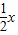 ,
,∴y=
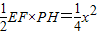 .
.∵PH≤DG,
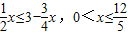 .
.当点P在四边形BCFE的外部时,如图2,
过点P作PH⊥EF于H,交MN于K,同理得PH=
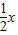 ,
,∵EF∥BC,
∴∠KHG=∠HKD=90°,
∴四边形HGDK为矩形,
∴HK=DG=3-
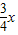 ,
,∴PK=
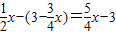 ,
,∵EF∥BC,
∴△PMN∽△PEF,
∴
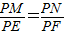 ,
,∴△PMN为等腰直角三角形.
∴S△PMN=
 MN×PK=PK2=
MN×PK=PK2=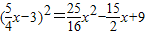 ,
,∴
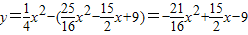 ,
,∵PH>DG,
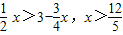
∴
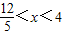 .
.点评:此题多次用到三角形相似的性质,这也是平面几何题通常用的方法,作辅助线找三角形相似,把几何关系用函数表示出来,并求出定义域,是很好的题型.

练习册系列答案
相关题目
 15、如图,△ABC的高AD、BE、CF相交于点I,△BIC的BI边上的高是
15、如图,△ABC的高AD、BE、CF相交于点I,△BIC的BI边上的高是 23、如图,△ABC的高BD、CE相交于点O,且OB=OC,AB与AC相等吗?为什么?
23、如图,△ABC的高BD、CE相交于点O,且OB=OC,AB与AC相等吗?为什么? 10、如图,△ABC的高AD、BE相交于点O,则∠C与∠BOD的关系是( )
10、如图,△ABC的高AD、BE相交于点O,则∠C与∠BOD的关系是( ) 如图,△ABC的高CF、BG相交于点H,分别延长CF、BG与△ABC的外接圆交于D、E两点,则下列结论:①AD=AE;②AH=AE;③若DE为△ABC的外接圆的直径,则BC=AE.其中正确的是( )
如图,△ABC的高CF、BG相交于点H,分别延长CF、BG与△ABC的外接圆交于D、E两点,则下列结论:①AD=AE;②AH=AE;③若DE为△ABC的外接圆的直径,则BC=AE.其中正确的是( ) 如图,△ABC的高AD=4,BC=8,四边形MNPQ是△ABC中任意一个内接矩形
如图,△ABC的高AD=4,BC=8,四边形MNPQ是△ABC中任意一个内接矩形