题目内容
 如图,已知菱形ABCD的边AB=10,对角线BD=12,BD边上有2012个不同的点P1,P2,…,P2012,过Pi(i=1,2,…,2012)作PiEi⊥AB于Ei,PiFi⊥AD于Fi,则P1E1+P1F1+P2E2+P2F2+…+P2012E2012+P2012F2012的值为________.
如图,已知菱形ABCD的边AB=10,对角线BD=12,BD边上有2012个不同的点P1,P2,…,P2012,过Pi(i=1,2,…,2012)作PiEi⊥AB于Ei,PiFi⊥AD于Fi,则P1E1+P1F1+P2E2+P2F2+…+P2012E2012+P2012F2012的值为________.
19315.2
分析:作点E1关于BD的对称点M,则根据菱形的性质可得点M、P1、F1在一条直线上,且MF1⊥BC,从而可得PiEi+PiFi等于菱形两边BC与AD之间的距离,结合题意所给条件即可得出答案.
解答:
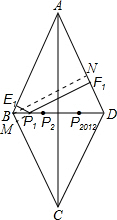
作点E1关于BD的对称点M,则P1M⊥BC,
又∵P1F⊥BC,
∴M、P1、F1在一条直线上,且MF1⊥BC,
故可得PiEi+PiFi等于菱形两边BC与AD之间的距离,
又∵AO= =8,AC=2AO=16,
=8,AC=2AO=16,
∴BN=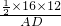 =9.6,
=9.6,
故可得:P1E1+P1F1+P2E2+P2F2+…+P2012E2012+P2012F2012=2012×9.6=19315.2.
故答案为:19315.2.
点评:此题考查了菱形的性质,根据菱形的性质得出PiEi+PiFi等于菱形两边BC与AD之间的距离是解答本题的关键,有一定难度.
分析:作点E1关于BD的对称点M,则根据菱形的性质可得点M、P1、F1在一条直线上,且MF1⊥BC,从而可得PiEi+PiFi等于菱形两边BC与AD之间的距离,结合题意所给条件即可得出答案.
解答:

作点E1关于BD的对称点M,则P1M⊥BC,
又∵P1F⊥BC,
∴M、P1、F1在一条直线上,且MF1⊥BC,
故可得PiEi+PiFi等于菱形两边BC与AD之间的距离,
又∵AO=
 =8,AC=2AO=16,
=8,AC=2AO=16,∴BN=
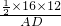 =9.6,
=9.6,故可得:P1E1+P1F1+P2E2+P2F2+…+P2012E2012+P2012F2012=2012×9.6=19315.2.
故答案为:19315.2.
点评:此题考查了菱形的性质,根据菱形的性质得出PiEi+PiFi等于菱形两边BC与AD之间的距离是解答本题的关键,有一定难度.

练习册系列答案
相关题目
 如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
 如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
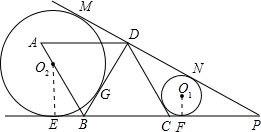 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G. 如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的
如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的