题目内容
 如图,Rt△ABC中AB=3,BC=4,∠B=90°,点B、C在两坐标轴上滑动.当边AC⊥x轴时,点A刚好在双曲线
如图,Rt△ABC中AB=3,BC=4,∠B=90°,点B、C在两坐标轴上滑动.当边AC⊥x轴时,点A刚好在双曲线 上,此时下列结论不正确的是
上,此时下列结论不正确的是
- A.点B为(0,
 )
) - B.AC边的高为

- C.双曲线为
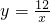
- D.此时点A与点O距离最大
D
分析:根据AB=3,BC=4,∠B=90°,利用勾股定理可求AC=5,而AC⊥x轴,易知点A的纵坐标是5,设AC边上的高是h,再结合三角形的面积公式,易求h,进而可得点A的坐标,再代入反比例函数解析式,易求k,从而可得反比例函数解析式,在Rt△BOC中,利用勾股定理可求OB,从而可得点B的坐标.综上可知A、B、C都正确,从而选择D.
解答:∵ AB=3,BC=4,∠B=90°,
AB=3,BC=4,∠B=90°,
∴AC=5,
∵AC⊥x轴,
∴点A的纵坐标是5,
设AC边上的高是h,
∵S△ABC= ×3×4=
×3×4= ×5•h,
×5•h,
∴h= ;
;
∴点A的坐标是( ,5),
,5),
又∵点A在 上,
上,
∴k=12,
∴反比例函数的解析式是y= ;
;
∵OC= ,BC=4,
,BC=4,
∴OB= (负数舍去),
(负数舍去),
∴B点坐标是(0, ).
).
综上所述,可知ABC都是正确的,答案D不一定正确,利用排除法可知.
故选D.
点评:本题考查了反比例函数综合题,解题的关键是掌握点与函数解析式之间的密切关系,灵活掌握三角形面积的计算、勾股定理的使用.
分析:根据AB=3,BC=4,∠B=90°,利用勾股定理可求AC=5,而AC⊥x轴,易知点A的纵坐标是5,设AC边上的高是h,再结合三角形的面积公式,易求h,进而可得点A的坐标,再代入反比例函数解析式,易求k,从而可得反比例函数解析式,在Rt△BOC中,利用勾股定理可求OB,从而可得点B的坐标.综上可知A、B、C都正确,从而选择D.
解答:∵
 AB=3,BC=4,∠B=90°,
AB=3,BC=4,∠B=90°,∴AC=5,
∵AC⊥x轴,
∴点A的纵坐标是5,
设AC边上的高是h,
∵S△ABC=
 ×3×4=
×3×4= ×5•h,
×5•h,∴h=
 ;
;∴点A的坐标是(
 ,5),
,5),又∵点A在
 上,
上,∴k=12,
∴反比例函数的解析式是y=
 ;
;∵OC=
 ,BC=4,
,BC=4,∴OB=
 (负数舍去),
(负数舍去),∴B点坐标是(0,
 ).
).综上所述,可知ABC都是正确的,答案D不一定正确,利用排除法可知.
故选D.
点评:本题考查了反比例函数综合题,解题的关键是掌握点与函数解析式之间的密切关系,灵活掌握三角形面积的计算、勾股定理的使用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.