题目内容
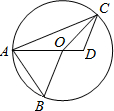如图，A、B、C均为⊙O上的点，D是AO延长线上一点，若∠CAB=78°，CD∥OB，∠COD=46°，则∠D为________度．
110
分析：延长CD交⊙O于点E．根据圆周角定理求得∠COB=2∠CAB=156°；然后由图形中角与角间的和差关系、平行线的性质可以求得∠BOD=∠CDO=110°．
解答：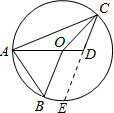
解：延长CD交⊙O于点E．
∵∠CAB=78°（已知），
∴∠COB=2∠CAB=156°（同弧所对的圆周角是圆心角的一半）；
又∵∠COD=46°（已知），
∴∠BOD=∠COB-∠COD=156°-46°=110°；
∵CD∥OB（已知），
∴∠BOD=∠CDO=110°（两直线平行，内错角相等）；
故答案为：110°．
点评：本题考查了平行线的性质、圆周角定理．本题通过作辅助线CE构建两平行线间的内错角相等来解答问题的．
分析：延长CD交⊙O于点E．根据圆周角定理求得∠COB=2∠CAB=156°；然后由图形中角与角间的和差关系、平行线的性质可以求得∠BOD=∠CDO=110°．
解答：
解：延长CD交⊙O于点E．∵∠CAB=78°（已知），
∴∠COB=2∠CAB=156°（同弧所对的圆周角是圆心角的一半）；
又∵∠COD=46°（已知），
∴∠BOD=∠COB-∠COD=156°-46°=110°；
∵CD∥OB（已知），
∴∠BOD=∠CDO=110°（两直线平行，内错角相等）；
故答案为：110°．
点评：本题考查了平行线的性质、圆周角定理．本题通过作辅助线CE构建两平行线间的内错角相等来解答问题的．
练习册系列答案
相关题目
如图，四边形ABCD和四边形EFGB均为正方形，点E在AB边的中点，若正方形ABCD的边长为1，则△AFC的面积等于
如图，小正方形的边长均为1，则下面图中的三角形（阴影部分）与△ABC相似的是（ ）
（2012•江西模拟）如图，A、B、C均为⊙O上的点，D是AO延长线上一点，若∠CAB=78°，CD∥OB，∠COD=46°，则∠D为
已知：如图所示，△ABC，△DEF均为锐角三角形，AB=DE，AC=DF，∠B=∠E．求证：△ABC≌△DEF．