题目内容
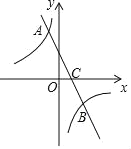
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(
(m≠0)交于点A(![]() ,2)B(1,﹣1).
,2)B(1,﹣1).
(1)方程kx+b﹣![]() =0的解为 ,不等式
=0的解为 ,不等式![]() 的解集是 ;(请直接写出答案)
的解集是 ;(请直接写出答案)
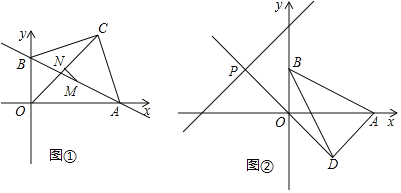
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
【答案】(1)x=﹣![]() 或1;﹣
或1;﹣![]() <x<0或x>1;(2)点P的坐标为(﹣
<x<0或x>1;(2)点P的坐标为(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)结合图象,分析函数值的大小关系即可;(2)用待定系数法求直线解析式;设点P的坐标为(x,0),则PC=|x﹣![]() |,根据面积公式求解.
|,根据面积公式求解.
解:(1)当x=﹣![]() 或x=1时,kx+b=
或x=1时,kx+b=![]() ,所以方程kx+b﹣
,所以方程kx+b﹣![]() =0的解为x=﹣
=0的解为x=﹣![]() 或1;
或1;
当﹣![]() <x<0或x>1时,kx+b<
<x<0或x>1时,kx+b<![]() ,则不等式kx+b<
,则不等式kx+b<![]() 的解集是﹣
的解集是﹣![]() <x<0或x>1;
<x<0或x>1;
故答案为x=﹣![]() 或1;﹣
或1;﹣![]() <x<0或x>1;
<x<0或x>1;
(2)把A(![]() ,2)B(1,﹣1)代入y=kx+b得
,2)B(1,﹣1)代入y=kx+b得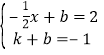 ,解得
,解得![]() ,则直线解析式为y=﹣2x﹣1,
,则直线解析式为y=﹣2x﹣1,
当x=0时,﹣2x+1=0,解得x=![]() ,则C(
,则C(![]() ,0),
,0),
设点P的坐标为(x,0),则PC=|x﹣![]() |,
|,
∵S△ABP=3,
∴![]() ×3|x﹣
×3|x﹣![]() |=3,即|x﹣
|=3,即|x﹣![]() |=2,
|=2,
解得:x1=﹣![]() ,x2=
,x2=![]() ,
,
∴点P的坐标为(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).

练习册系列答案
相关题目
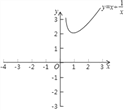
【题目】某数学兴趣小组对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | m | ﹣2 | - | - |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 ,m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+![]() =3有 个实数根;
=3有 个实数根;
②若关于x的方程x+![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 .