题目内容
已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,
点A的对应点C恰好落在⊙O上.
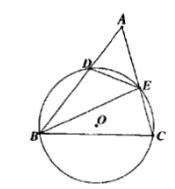
(1)当P在AB上方而C在AB下方时(如图1),判断PO与BC的位置关系,并证明你的判断;
(2)当P、C都在AB上方时(如图2),过C点作CD⊥直线AP于D,且PC=2PD,证明:CD是⊙O的切线.
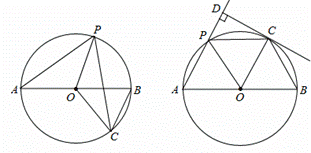
图1 图2
解:(1)结论PO∥BC成立,理由为.
由折叠可知:△APO≌△CPO,
∴∠APO=∠CPO,
又OA=OP,∴∠A=∠APO,∴∠A=∠CPO.
又∠A与∠PCB都是 所对的圆周角,
所对的圆周角,
∴∠A=∠PCB,∴∠CPO=∠PCB, ∴PO∥BC;
(2)在Rt△PCD中, ,
,
 因为△AOP沿OP对折,点A的对应点C恰好落在⊙O上,所以
因为△AOP沿OP对折,点A的对应点C恰好落在⊙O上,所以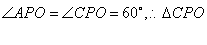 为等边三角形,
为等边三角形,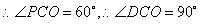 ,DC经过半径OC的外端C,所以DC为圆O的切线.
,DC经过半径OC的外端C,所以DC为圆O的切线.
(或者(1)结论PO∥BC成立,理由为.
由折叠可知:△APO≌△CPO,
∴∠APO=∠CPO,
又OA=OP,∴∠A=∠APO,∴∠A=∠CPO.
又∠A与∠PCB都是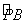 所对的圆周角,
所对的圆周角,
∴∠A=∠PCB,∴∠CPO=∠PCB, ∴PO∥BC;
(2)在Rt△PCD中, ,∴∠DCP=30°, ∠DPC=60°.
,∴∠DCP=30°, ∠DPC=60°.
又∠APO=∠CPO,且∠APO+∠CPO+∠DPC=180°,
∴∠APO=∠CPO=60°.
又OA=OP=OC,∴△OAP和△OCP均为等边三角形.
∴∠OCP=60°.又∠DCP=30°,
∴∠OCD=90°,即OC⊥CD.
∴CD是⊙O的切线.)

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
 ﹣
﹣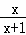 )÷
)÷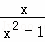 ,再在﹣3<x≤2中取一个合适的x,求出此时分式的值
,再在﹣3<x≤2中取一个合适的x,求出此时分式的值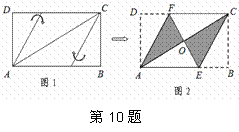
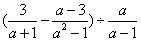 .其中2sin30°≤ a ≤ 3cos30°,且a为整数.
.其中2sin30°≤ a ≤ 3cos30°,且a为整数.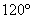 圆心角所对的弧长是
圆心角所对的弧长是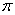 B.
B. 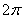 C.
C. 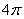
 D.
D. 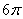
 二次函数
二次函数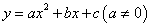 图象的一部分,对称轴是直线
图象的一部分,对称轴是直线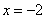 .关于下列结论:①
.关于下列结论:① 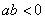 ;②
;② 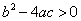 ;③
;③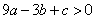 ;④
;④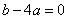 ;⑤方程
;⑤方程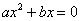 的两个根为
的两个根为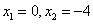 ,其中正确的结论有
,其中正确的结论有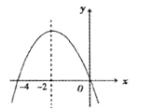
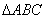 中,
中,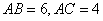 ,点
,点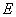 为
为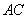 边上的一点(不与点
边上的一点(不与点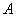 重合),过
重合),过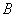 ,
,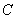 ,
,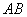 边交于点
边交于点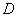 ,连接
,连接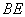 .设
.设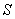 ,
,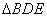 BDE的面积为
BDE的面积为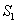 .
. 时,求
时,求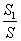 的值;
的值;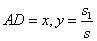 ;
;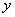 与
与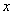 的函数表达式
的函数表达式 ,并写出自变量
,并写出自变量