题目内容
3．（1）先化简，再求代数式$\frac{a}{a+2}-\frac{1}{a-1}÷\frac{a+2}{{a}^{2}-2a+1}$的值，其中a=$\frac{2}{3}$．（2）已知$\frac{5x-4}{（x-5）（x+2）}=\frac{A}{x-5}+\frac{B}{x+2}$，求A、B的值．
分析 （1）先根据分式混合运算的法则把原式进行化简，再把a的值代入进行计算即可；
（2）先把等式的右边通分，再与左边相比较即可得出结论．
解答 解：（1）原式=$\frac{a}{a+2}$-$\frac{1}{a-1}$•$\frac{（a-1）^{2}}{a+2}$
=$\frac{a}{a+2}$-$\frac{a-1}{a+2}$
=$\frac{1}{a+2}$，
当a=$\frac{2}{3}$时，原式=$\frac{1}{\frac{2}{3}+2}$=$\frac{3}{8}$；
（2）右边=$\frac{A（x+2）+B（x-5）}{（x-5）（x+2）}$
=$\frac{（A+B）x+（2A-5B）}{（x-5）（x+2）}$，
∴A+B=5，2A-5B=5，
解得A=3，B=2．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
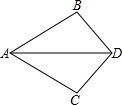如图，已知AB=AC，请你添加一个条件：BD=CD，使△ABD≌△ACD．