题目内容
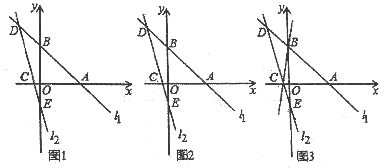
【题目】如图所示，在平面直角坐标系中，已知
，
，
．
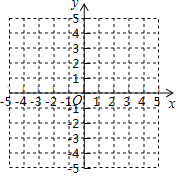
（1）在图中画出
，的面积是_____________；
（2）若点
与点
关于
轴对称，则点的坐标为_____________；
（3）已知
为轴上一点，若
的面积为
，求点的坐标．
【答案】（1）4；（2）
；（3）
或
【解析】
（1）根据指标坐标系中点的位置画出△ABC，作C垂直于y轴直线垂足为E, 作C垂直于x轴直线垂足为F,△ABC的面积等于矩形CEOF减去△CEA，△ABO,△BCF即可.
（2）根据对称轴的性质求出D坐标即可；
（3）△ACQ的高是CE为4，根据面积公式求出AQ，注意Q点为两组坐标.
解：（1）如图所示：S△ABC=S矩形CEOF-S△ABO-S△CEA-S△BCF
= 
；
故答案为：
；
（2）点
与点
关于
轴对称，则点的坐标为：；
故答案为：；
（3）
为
轴上一点，
的面积为
，
，
故
点坐标为：或．
练习册系列答案
相关题目
【题目】抛物线y=ax2+bx+c（a≠0）中自变量x和函数值y的部分对应值如下表：
x | … | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| … |
y | … | ﹣ | ﹣2 | ﹣ | ﹣2 | ﹣ | 0 |
| … |
从上表可知，下列说法正确的个数是（ ）
①抛物线与x轴的一个交点为（﹣2，0）；
②抛物线与y轴的交点为（0，﹣2）；
③抛物线的对称轴是：x=1；
④在对称轴左侧，y随x增大而增大．
A. 1 B. 2 C. 3 D. 4
