题目内容
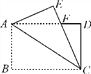
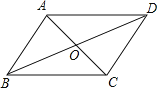
【题目】如图,AD是![]() 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).
的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).

A.2.5B.2C.1.5D.1
【答案】C
【解析】
延长AD,使DG=AD,连接BG,由“SAS”可证△ADC≌△GDB,可得AC=DG=CF+AF=6+AF,∠DAC=∠G,由等腰三角形的性质可得BE=BG=7.5,即可求EF的长.
解:如图,延长AD,使DG=AD,连接BG,

∵AD是△ABC的中线,
∴BD=CD,且DG=AD,∠ADC=∠BDG,
∴△ADC≌△GDB(SAS),
∴AC=DG=CF+AF=6+AF,∠DAC=∠G,
∵EF=AF,
∴∠DAC=∠AEF,
∴∠G=∠AEF=∠BEG,
∴BE=BG=7.5,
∴6+AF=BG=7.5,
∴AF=1.5=EF,
故选择:C.

练习册系列答案
相关题目