题目内容
 图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=
图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=
- A.

- B.

- C.

- D.

D
分析:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F,则易证AO⊥BE,△BOF∽△AOB,则sin∠CBE= ,求得OF的长即可求解.
,求得OF的长即可求解.
解答: 解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F
解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F
∵AB,AE都为圆的切线
∴AE=AB
∵OB=OE,AO=AO
∴△ABO≌△AEO(SSS)
∴∠OAB=∠OAE
∴AO⊥BE
在直角△AOB里AO2=OB2+AB2
∵OB=1,AB=3
∴AO=
易证明△BOF∽△AOB
∴BO:AO=OF:OB
∴1: =OF:1
=OF:1
∴OF=
sin∠CBE= =
=
故选D.
点评:本题主要考查了切线长定理,以及三角形的相似,求角的三角函数值的问题转化为求线段的比的问题.
分析:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F,则易证AO⊥BE,△BOF∽△AOB,则sin∠CBE=
 ,求得OF的长即可求解.
,求得OF的长即可求解.解答:
 解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F
解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F∵AB,AE都为圆的切线
∴AE=AB
∵OB=OE,AO=AO
∴△ABO≌△AEO(SSS)
∴∠OAB=∠OAE
∴AO⊥BE
在直角△AOB里AO2=OB2+AB2
∵OB=1,AB=3
∴AO=

易证明△BOF∽△AOB
∴BO:AO=OF:OB
∴1:
 =OF:1
=OF:1∴OF=

sin∠CBE=
 =
=
故选D.
点评:本题主要考查了切线长定理,以及三角形的相似,求角的三角函数值的问题转化为求线段的比的问题.

练习册系列答案
相关题目
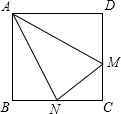 如图,在矩形ABCD中,M为CD上一点,沿AM折叠,使D点落在BC上的N点处,如果AD=
如图,在矩形ABCD中,M为CD上一点,沿AM折叠,使D点落在BC上的N点处,如果AD= 如图,在矩形ABCD中,AB=9,
如图,在矩形ABCD中,AB=9, 12、如图,在矩形ABCD中,AB=3,AD=5,点P在线段BC上运动,现将纸片折叠,使点A与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),设BP=x,当点E落在AB上,点F落在AD上时,x的取值范围是( )
12、如图,在矩形ABCD中,AB=3,AD=5,点P在线段BC上运动,现将纸片折叠,使点A与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),设BP=x,当点E落在AB上,点F落在AD上时,x的取值范围是( ) 如图,在矩形ABCD中,E、H、G、F分别为边AB、BC、CD、DA的中点,若AB=3,AD=4,则图中四边形EFGH的面积为( )
如图,在矩形ABCD中,E、H、G、F分别为边AB、BC、CD、DA的中点,若AB=3,AD=4,则图中四边形EFGH的面积为( ) (2012•内江)如图,在矩形ABCD中,AB=10,BC=5,点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A1、D1处,则阴影部分图形的周长为( )
(2012•内江)如图,在矩形ABCD中,AB=10,BC=5,点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A1、D1处,则阴影部分图形的周长为( )