Question

【题目】如图,已知…是轴上的点，且…，分别过点…作轴的垂线交反比例函数的图象于点…,过点作于点,过点作于点……记的面积为,的面积为……的面积为，则…等于_________．

Answer 1

【答案】

【解析】

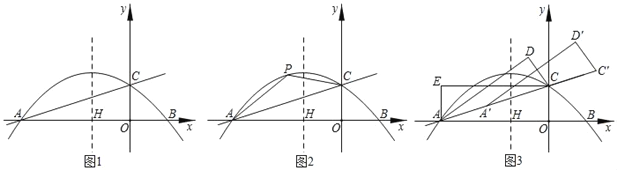
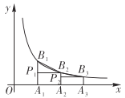
由OA1=A1A2=A2A3=…=AnAn+1=1可知B1点的坐标为（1，y1），B2点的坐标为（2，y2），B3点的坐标为（3，y3）…Bn点的坐标为（n，yn），Bn+1点的坐标为（n+1，yn+1），把x=1，x=2，x=3代入反比例函数的解析式即可求出y1、y2、y3的值，再由三角形的面积公式可得出S1、S2、S3…Sn的值，故可得出结论．

解：∵OA1=A1A2=A2A3=…=AnAn+1=1，

∴设B1(1,y1),B2(2,y2),B3(3,y3),…Bn(n,yn)，Bn+1（n+1，yn+1），

∵B1,B2,B3…Bn，Bn+1在反比例函数的图象上，

∴y1=1,y2=,y3=，…，yn=，yn+1=，

∴S1=×1×(y1y2)=×1×(1)=(1)；

S2=×1×(y2y3)=×()；

S3=×1×(y3y4)= ×()；

…

Sn= ()，

∴S1+S2+S3+…+Sn=(1+++…+)=(1-)=.

故答案为：.