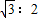题目内容
 甲题:已知x1、x2是关于x的一元二次方程x2-2x+a-1=0的两个实数根
甲题:已知x1、x2是关于x的一元二次方程x2-2x+a-1=0的两个实数根(1)若x1+2x2=3-
| 2 |
(2)若s=ax1x2+3x1+3x2-3a,求s的取值范围.
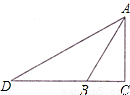
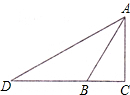
乙题:如图,在Rt△ABC中,∠C=90°,AC:AB=
| 3 |
(1)求BC:AC的值;
(2)延长CB到点D,使DB:DC=2:3,连接AD.
①求∠D的度数;②若AD=12,求△ABC三边的长.
解:我选做
甲
甲
题.分析:(1)先根据根与系数的关系得出x1+x2=2,再根据x1+2x2=3-
,求出x2,x1的值,再根据根与系数的关系即可求出a的值;
(2)根据根与系数的关系把x1x2=a-1,x1+x2=2代入s=ax1x2+3x1+3x2-3a,然后把所得的结果进行配方,即可得出s的取值范围.
| 2 |
(2)根据根与系数的关系把x1x2=a-1,x1+x2=2代入s=ax1x2+3x1+3x2-3a,然后把所得的结果进行配方,即可得出s的取值范围.
解答:解:我选做甲题:
(1)∵x1、x2是关于x的一元二次方程x2-2x+a-1=0的两个实数根,
∴x1+x2=2,
∵x1+2x2=3-
,
∴x2=1-
,x1=1+
,
∴a-1=(1+
)(1-
)=-1,
∴a=0;
(2)∵s=ax1x2+3x1+3x2-3a,
∴s=a(a-1)+3×2-3=a2-a+3=(a-
)2+
,
∴s的取值范围是s≥
.
故答案为:甲.
(1)∵x1、x2是关于x的一元二次方程x2-2x+a-1=0的两个实数根,
∴x1+x2=2,
∵x1+2x2=3-
| 2 |
∴x2=1-
| 2 |
| 2 |
∴a-1=(1+
| 2 |
| 2 |
∴a=0;
(2)∵s=ax1x2+3x1+3x2-3a,
∴s=a(a-1)+3×2-3=a2-a+3=(a-
| 1 |
| 2 |
| 11 |
| 4 |
∴s的取值范围是s≥
| 11 |
| 4 |
故答案为:甲.
点评:此题考查了根与系数的关系,关键根据根与系数的关系列出式子,再进行求解,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分.
(2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分.
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.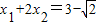 ,求x1、x2及a的值;
,求x1、x2及a的值;