题目内容
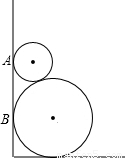
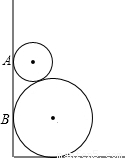
如图所示,两圆轮叠靠在墙边,已知两轮半径分别为4和1,则它们与墙的切点A,B间的距离为 .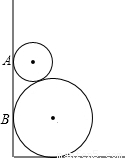
【答案】分析:此题要求AB之间的距离,只要将图形转化成直角三角形,利用勾股定理来求解即可.
解答: 解:设两圆圆心为O1,O2,连接O1,O2,作平行于AB且过点O1的直线,
解:设两圆圆心为O1,O2,连接O1,O2,作平行于AB且过点O1的直线,
根据勾股定理可得,|AB|2=O1O22-(R-r)2=25-9=16,
∴|AB|=4,
因此,A、B间的距离为4.
点评:此题考查的是根据题意构造直角三角形,再利用直角三角形的性质求解.
解答:
 解:设两圆圆心为O1,O2,连接O1,O2,作平行于AB且过点O1的直线,
解:设两圆圆心为O1,O2,连接O1,O2,作平行于AB且过点O1的直线,根据勾股定理可得,|AB|2=O1O22-(R-r)2=25-9=16,
∴|AB|=4,
因此,A、B间的距离为4.
点评:此题考查的是根据题意构造直角三角形,再利用直角三角形的性质求解.

练习册系列答案
相关题目
 24、如图所示,两圆轮叠靠在墙边,已知两轮半径分别为4和1,则它们与墙的切点A,B间的距离为
24、如图所示,两圆轮叠靠在墙边,已知两轮半径分别为4和1,则它们与墙的切点A,B间的距离为 如图所示,两圆轮叠靠在墙边,已知两圆轮半径分别为1和4,则它们与墙的切点A、B间的距离为
如图所示,两圆轮叠靠在墙边,已知两圆轮半径分别为1和4,则它们与墙的切点A、B间的距离为