题目内容
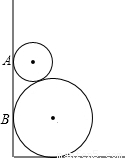
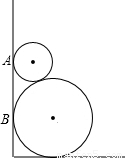
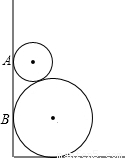
如图所示，两圆轮叠靠在墙边，已知两圆轮半径分别为1和4，则它们与墙的切点A、B间的距离为4
4
．分析：利用相切两圆的性质以及切线的性质得出四边形ABED是矩形，进而利用勾股定理得出AB的长．
解答：
解：如图所示：连接DF，DA，BF，过点D作DE⊥BF于点E，
由题意可得出：四边形ABED是矩形，
∵两圆轮半径分别为1和4，
∴AB=DE，EF=3，DF=5，
∴DE=AB=4．
故答案为：4．
解：如图所示：连接DF，DA，BF，过点D作DE⊥BF于点E，由题意可得出：四边形ABED是矩形，
∵两圆轮半径分别为1和4，
∴AB=DE，EF=3，DF=5，
∴DE=AB=4．
故答案为：4．
点评：此题主要考查了相切两圆的性质以及切线的性质和勾股定理等知识，根据题意得出四边形ABED是矩形是解题关键．
练习册系列答案
相关题目
24、如图所示，两圆轮叠靠在墙边，已知两轮半径分别为4和1，则它们与墙的切点A，B间的距离为
