题目内容
(2013年四川广安6分)已知反比例函数 (k≠0)和一次函数y=x﹣6.
(k≠0)和一次函数y=x﹣6.
(1)若一次函数与反比例函数的图象交于点P(2,m),求m和k的值.
(2)当k满足什么条件时,两函数的图象没有交点?
【答案】
解:(1)∵一次函数和反比例函数的图象交于点P(2,m),∴m=2﹣6,解得m=﹣4。
∴点P(2,﹣4)。
将点P(2,﹣4)代入 ,得k=2×(﹣4)=﹣8。
,得k=2×(﹣4)=﹣8。
∴m=﹣4,k=﹣8。
(2)联立反比例函数 和一次函数y=x﹣6,得
和一次函数y=x﹣6,得 ,即x2﹣6x﹣k=0。.
,即x2﹣6x﹣k=0。.
∵要使两函数的图象没有交点,须使方程x2﹣6x﹣k=0无解,
∴△=(﹣6)2﹣4×(﹣k)=36+4k<0,解得k<﹣9。
∴当k<﹣9时,两函数的图象没有交点。
【解析】(1)两个函数交点的坐标满足这两个函数关系式,因此将交点的坐标分别代入反比例函数关系式和一次函数关系式即可求得待定的系数;
(2)函数的图象没有交点,则联立的方程组无解,从而用一元二次方程根的判别式可解。
考点:反比例函数与一次函数的交点问题,曲线上点的坐标与方程的关系。

练习册系列答案
相关题目
(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
|
|
空调 |
彩电 |
|
进价(元/台) |
5400 |
3500 |
|
售价(元/台) |
6100 |
3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
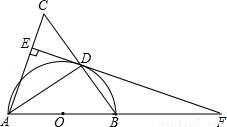
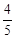 ,求BF的长.
,求BF的长.