题目内容
如图,已知点O是△ABC内一点,且点O到三边的距离相等,∠A=40°,对∠BOC=

- A.110°
- B.120°
- C.130°
- D.140°
A
分析:由已知,O到三角形三边距离相等,得O是内心,再利用三角形内角和定理即可求出∠BOC的度数.
解:由已知,O到三角形三边距离相等,所以O是内心,
即三条角平分线交点,AO,BO,CO都是角平分线,
所以有∠CBO=∠ABO= ∠ABC,∠BCO=∠ACO=
∠ABC,∠BCO=∠ACO=![]() ∠ACB,
∠ACB,
∠ABC+∠ACB=180-40=140
∠OBC+∠OCB=70
∠BOC=180-70=110°
故选A.
分析:由已知,O到三角形三边距离相等,得O是内心,再利用三角形内角和定理即可求出∠BOC的度数.
解:由已知,O到三角形三边距离相等,所以O是内心,
即三条角平分线交点,AO,BO,CO都是角平分线,
所以有∠CBO=∠ABO=
 ∠ABC,∠BCO=∠ACO=
∠ABC,∠BCO=∠ACO=∠ABC+∠ACB=180-40=140
∠OBC+∠OCB=70
∠BOC=180-70=110°
故选A.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
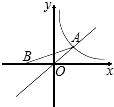 如图,已知点A是函数y=x与y=
如图,已知点A是函数y=x与y=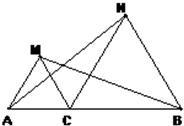 20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.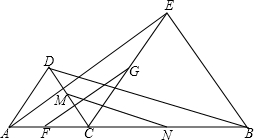 M、N分别是线段AC、CE、CD、CB的中点,
M、N分别是线段AC、CE、CD、CB的中点,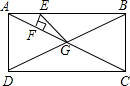 如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=
如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG= 如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.
如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.