题目内容
 如图,已知等腰梯形ABCD中,AD=BC=DC=1,AB=AC,那么底边AB的长为
如图,已知等腰梯形ABCD中,AD=BC=DC=1,AB=AC,那么底边AB的长为
- A.

- B.

- C.
 或
或
- D.2
B
分析:过C作CE∥AD交AB于E,得出AECD为菱形,再由边角关系得出△ABC∽△CBE,进而对应边成比例,即可求解.
解答: 解:如图,过C作CE∥AD交AB于E.
解:如图,过C作CE∥AD交AB于E.
所以四边形AECD为平行四边形
又因为AD=BC=DC=1,
所以平行四边形AECD为菱形,CD=AE=EC=1,
所以∠B=∠CEB
又因为AB=AC,
所以∠B=∠BCA
所以∠CEB=∠BCA,
因为∠B为公共角,
所以△ABC∽△CBE,
设AB=x,则BE=x-1
所以
所以x2-x-1=0,
因为x>0
所以x=
所以AB=
故选B.
点评:本题主要考查了菱形的判定及性质以及相似三角形的判定及性质问题,能够熟练掌握.
分析:过C作CE∥AD交AB于E,得出AECD为菱形,再由边角关系得出△ABC∽△CBE,进而对应边成比例,即可求解.
解答:
 解:如图,过C作CE∥AD交AB于E.
解:如图,过C作CE∥AD交AB于E.所以四边形AECD为平行四边形
又因为AD=BC=DC=1,
所以平行四边形AECD为菱形,CD=AE=EC=1,
所以∠B=∠CEB
又因为AB=AC,
所以∠B=∠BCA
所以∠CEB=∠BCA,
因为∠B为公共角,
所以△ABC∽△CBE,

设AB=x,则BE=x-1
所以

所以x2-x-1=0,
因为x>0
所以x=

所以AB=

故选B.
点评:本题主要考查了菱形的判定及性质以及相似三角形的判定及性质问题,能够熟练掌握.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 ,
, 3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( )
3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( ) 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为
13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为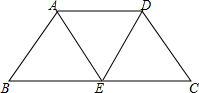 如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是
如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是