题目内容
 四边形ABCD的四条边长AB=
四边形ABCD的四条边长AB= ,BC=5,CD=3,AD=2,∠D为直角,则∠A的外角的正切值为
,BC=5,CD=3,AD=2,∠D为直角,则∠A的外角的正切值为
- A.

- B.

- C.

- D.

B
分析:连接AC,作射线BA,分别求出AC、AB、BC的平方,得出BC2=AB2+AC2,推出∠BAC=90°,求出∠A的外角等于∠DCA,求出∠DCA的正切值即可.
解答:连接AC,作射线BA,如图,
∵在Rt△ADC中,由勾股定理得:AC2=AD2+DC2=22+32=13,
又∵AB2=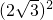 =12,BC2=52=25,
=12,BC2=52=25,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∵∠D=90°,
∴∠DAC+∠DCA=90°,
∵∠BAD的外角∠EAD=180°-90°-∠DAC,
∴∠BAD的外角的度数等于∠DCA的度数,
即tan∠DCA= =
= .
.
故选B.
点评:本题考查了直角梯形,勾股定理的逆定理,锐角三角函数的定义的应用,关键是求出∠A的外角等于∠DCA,题目具有一定的代表性,是一道比较好的题目.
分析:连接AC,作射线BA,分别求出AC、AB、BC的平方,得出BC2=AB2+AC2,推出∠BAC=90°,求出∠A的外角等于∠DCA,求出∠DCA的正切值即可.
解答:连接AC,作射线BA,如图,

∵在Rt△ADC中,由勾股定理得:AC2=AD2+DC2=22+32=13,
又∵AB2=
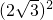 =12,BC2=52=25,
=12,BC2=52=25,∴BC2=AB2+AC2,
∴∠BAC=90°,
∵∠D=90°,
∴∠DAC+∠DCA=90°,
∵∠BAD的外角∠EAD=180°-90°-∠DAC,
∴∠BAD的外角的度数等于∠DCA的度数,
即tan∠DCA=
 =
= .
.故选B.
点评:本题考查了直角梯形,勾股定理的逆定理,锐角三角函数的定义的应用,关键是求出∠A的外角等于∠DCA,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
相关题目