Question

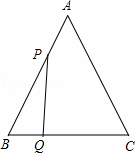
已知：如图，△ABC是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间t（s），解答下列各问题：

（1）求△ABC的面积；

（2）当t为何值时，△PBQ是直角三角形？

（3）设四边形APQC的面积为y（cm²），求y与t的关系式；是否存在某一时刻t，使四边形APQC的面积是△ABC面积的三分之二？如果存在，求出t的值；不存在请说明理由．

Answer 1

考点：

等边三角形的性质；一元二次方程的应用；勾股定理．.

专题：

动点型．

分析：

（1）过点A作AD⊥BC，求出AD的长，利用三角形的面积公式进行解答即可；

（2）①∠BPQ=90°；②∠BQP=90°．然后在直角三角形BQP中根据BP，BQ的表达式和∠B的度数进行求解即可．

（3）本题可先用△ABC的面积﹣△PBQ的面积表示出四边形APQC的面积，即可得出y，t的函数关系式，然后另y等于三角形ABC面积的三分之二，可得出一个关于t的方程，如果方程无解则说明不存在这样的t值，如果方程有解，那么求出的t值即可．

解答：

解：（1）过点A作AD⊥BC，则AD=×BC×AB•sin60°=×3×3×=；

（2）设经过t秒△PBQ是直角三角形，

则AP=tcm，BQ=tcm，

△ABC中，AB=BC=3cm，∠B=60°，

∴BP=（3﹣t）cm，

△PBQ中，BP=（3﹣t）cm，BQ=tcm，若△PBQ是直角三角形，则∠BQP=90°或∠BPQ=90°，

当∠BQP=90°时，BQ=BP，

即t=（3﹣t），t=1（秒），

当∠BPQ=90°时，BP=BQ，

3﹣t=t，t=2（秒），

答：当t=1秒或t=2秒时，△PBQ是直角三角形．

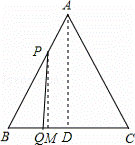
（3）过P作PM⊥BC于M，

△BPM中，sin∠B=，

∴PM=PB•sin∠B=（3﹣t），

∴S_△PBQ=BQ•PM=•t•（3﹣t），

∴y=S_△ABC﹣S_△PBQ=×3²×﹣×t×（3﹣t）

=t²﹣t+，

∴y与t的关系式为y=t²﹣t+，

假设存在某一时刻t，使得四边形APQC的面积是△ABC面积的，

则S_{四边形APQC}=S_△ABC，

∴t²﹣t+=××3²×，

∴t²﹣3t+3=0，

∵（﹣3）²﹣4×1×3＜0，

∴方程无解，

∴无论t取何值，四边形APQC的面积都不可能是△ABC面积的．

点评：

本题考查的是等边三角形的性质、直角三角形的判定及三角形的面积公式，根据题意作出辅助线，利用数形结合求解是解答此题的关键．