题目内容
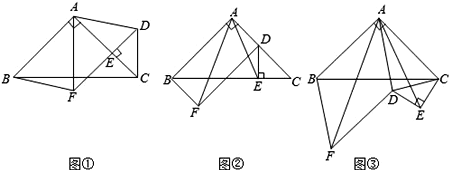
【题目】如图，正方形ABCD的边长为2，点O是正方形的中心，过点O作一条直线l分别交正方形AD，BC两边于点E，F.直线l将正方形分成两部分，将其中的一个部分沿这条直线翻折到另一个部分上，若AE＝
，则两个部分图形中不重叠部分的面积为_______．
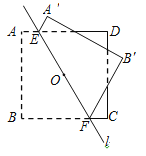
【答案】12－8
【解析】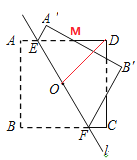
连接OD，因点O是正方形的中心，可求得OD=
，∠ODE=45° ，因AE＝2-
，正方形的边长是2，可求得DE=
，即可得OD=DE，根据等腰三角形的性质和三角形的内角和定理可得∠DEA=67.5°，根据对顶角相等和折叠的性质可得∠AEA’=135°，所以∠AEM=45°，△AEM是等腰直角三角形，根据条件易证这两个部分图形中不重叠部分的四个等腰直角三角形全等，即可得这两个部分图形中不重叠部分的面积为
.
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
【题目】为了更好治理某湖水质，保护环境，市治污公司决定购买
台污水处理设备．现有
，
两种型号的设备，其中每台的价格，月处理污水量如下表．经调查：购买一台型设备比购买一台型设备多
万元，购买台型设备比购买
台型设备少
万元．
|
| |
价格（万元/台） |
|
|
处理污水量（吨/月） |
|
|
（
）求
，
的值．
（）经预算：市治污公司购买污水处理设备的资金不超过
万元，你认为该公司有哪几种购买方案．
（）在（）问的条件下，若每月要求处理该湖的污水量不低于
吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．
