题目内容
 在矩形ABCD中,点E是AD的中点,EF⊥BE交CD于点F.
在矩形ABCD中,点E是AD的中点,EF⊥BE交CD于点F.
(1)当AB=BC时,求sin∠FBC;
(2)过F作GF⊥BF交BE的延长线于点G,求证: .
.
 (1)解:∵在矩形ABCD中,AB=BC,
(1)解:∵在矩形ABCD中,AB=BC,∴四边形ABCD是正方形,
∴AB=AD=CD=BC,∠A=∠D=90°,
∴∠AEB+∠ABE=90°,
∵EF⊥BE,
∴∠AEB+∠DEF=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF,
∴AB:DE=AE:DF,
∵点E是AD的中点,
∴DE=AE=
 AD=
AD= AB,
AB,∴DF=
 AB,
AB,∴CF=
 AB,
AB,∴BF=
 =
= AB,
AB,∴sin∠FBC=
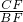 =
= ;
; (2)由(1)知△ABE∽△DEF,
(2)由(1)知△ABE∽△DEF,∴
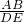 =
= =
=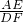 .
.设DE=AE=a,AB=CD=b,则AD=BC=2a.
∴
 =
= =
= ,
,∴DF=
 .
.在△BEF与△FEG中,
∵∠BFE=∠G=90°-∠EFG,∠BEF=∠FEG=90°,
∴△BEF∽△FEG,
∴BE:FE=EF:EG,
∵
 =
= ,∴可设EF=ak,则BE=bk(k≠0).
,∴可设EF=ak,则BE=bk(k≠0).∴EG=
 =
= =
= .
.∵
 =
= =
=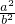 ,
, =
= =
=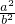 ,
,∴
 =
= .
.分析:(1)先由有一组邻边相等的矩形是正方形证明出四边形ABCD是正方形,得出AB=AD=CD=BC,再根据有两个角对应相等的三角形相似得出△ABE∽△DEF,由相似三角形对应边成比例得出AB:DE=AE:DF,然后根据三角函数的定义即可求出sin∠FBC;
(2)先由△ABE∽△DEF,得出
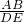 =
= =
=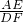 .设DE=AE=a,AB=CD=b,设EF=ak,则BE=bk(k≠0),则DF=
.设DE=AE=a,AB=CD=b,设EF=ak,则BE=bk(k≠0),则DF= .再由△BEF∽△FEG,得出BE:FE=EF:EG,则可用含a、b、k的代数式表示EG,然后分别计算
.再由△BEF∽△FEG,得出BE:FE=EF:EG,则可用含a、b、k的代数式表示EG,然后分别计算 ,
, ,即可得证.
,即可得证.点评:本题考查了矩形的性质,正方形与相似三角形的判定与性质,勾股定理,三角函数的定义,综合性较强,难度中等,(2)中设出辅助未知数可使解题简便.

练习册系列答案
相关题目
 1、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.线段DF与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.即DF=
1、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.线段DF与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.即DF=AB
.(写出一条线段即可) 14、如图所示,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,若AB=3,BC=5,则四边形DFEC的面积是( )
14、如图所示,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,若AB=3,BC=5,则四边形DFEC的面积是( )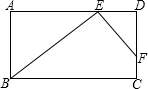
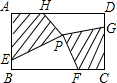 如图,在矩形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=4,BC=6,AE=CG=3,BF=DH=4,四边形AEPH的面积为5,求四边形PFCG的面积.
如图,在矩形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=4,BC=6,AE=CG=3,BF=DH=4,四边形AEPH的面积为5,求四边形PFCG的面积. (2013•泰州)如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
(2013•泰州)如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.