题目内容
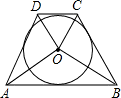如图，在⊙O的外切四边形ABCD中，AB=5，BC=4，CD=3，则S△AOB：S△BOC：S△COD：S△DOA=________．
5：4：3：4
分析：作圆心到各边的垂线，由切线长定理知，DA=DE，CE=CF，BF=BG，AS=AG，从而可求得AD的长；已知圆心到各边和距离相等，根据三角形的面积公式即可求得解．
解答：
解：如图，作圆心到各边的垂线；
∵DS=DE，CE=CF，BF=BG，AS=AG，
∴AD+BC=CD+AB，
∴AD=4，
∴S△AOB：S△BOC：S△COD：S△DOA=AB：BC：CD：AD=5：4：3：4．
点评：本题利用了切线长定理，三角形的面积公式求解．
分析：作圆心到各边的垂线，由切线长定理知，DA=DE，CE=CF，BF=BG，AS=AG，从而可求得AD的长；已知圆心到各边和距离相等，根据三角形的面积公式即可求得解．
解答：
解：如图，作圆心到各边的垂线；∵DS=DE，CE=CF，BF=BG，AS=AG，
∴AD+BC=CD+AB，
∴AD=4，
∴S△AOB：S△BOC：S△COD：S△DOA=AB：BC：CD：AD=5：4：3：4．
点评：本题利用了切线长定理，三角形的面积公式求解．
练习册系列答案
名校课堂系列答案
相关题目
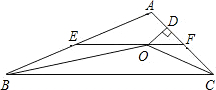交AC于F，过点O作OD⊥AC于D．下列四个结论：
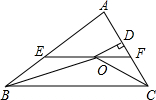如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：
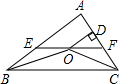如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC=90°+
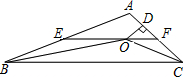如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：
如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：