题目内容
5.已知抛物线y=ax2+bx+5的顶点坐标为(-1,4),则a=1,b=2.分析 根据顶点坐标(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)可得出a,b的值.
解答 解:∵顶点坐标(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),
∴-$\frac{b}{2a}$=-1,$\frac{4ac-{b}^{2}}{4a}$=4,
∴a=1,b=2.
故答案为1,2.
点评 本题考查了二次函数的性质,根据抛物线的顶点坐标,列出关于a,b的方程组是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
13.下列方程是一元二次方程的是( )
| A. | 3x+1=0 | B. | 5x2-6y-3=0 | C. | ax2-x+2=0 | D. | 3x2-2x-1=0 |
20.把方程x(x+2)=5(x-2)化成一元二次方程的一般形式,则a、b、c的值分别是( )
| A. | 1,-3,10 | B. | 1,7,-10 | C. | 1,-5,12 | D. | 1,3,2 |
10.方程2x2-4=0的解是( )
| A. | x=2 | B. | x=-2 | C. | x=±2 | D. | x=$±\sqrt{2}$ |
14.下列说法错误的是( )
| A. | 0是最小的整数 | B. | 1是最小的正整数 | C. | 0是最小的自然数 | D. | 自然数是非负数 |
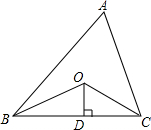 如图所示,已知△ABC的面积是26,AB+AC=20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=2,则BC的长是6.
如图所示,已知△ABC的面积是26,AB+AC=20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=2,则BC的长是6.