题目内容
汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内剩余油量Q(升)与行驶时间t(时)的关系用图象表示应为图中的( )
A. 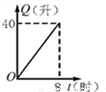 B.
B. 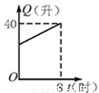 C.
C. 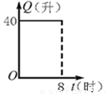 D.
D. 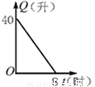
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
题目内容
汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内剩余油量Q(升)与行驶时间t(时)的关系用图象表示应为图中的( )
A.  B.
B.  C.
C.  D.
D. 
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案