Question

在△ABC中，BC=10，B₁、C₁分别是图①中AB、AC的中点，在图②中，B₁，B₂，C₁，C₂分别是AB，AC的三等分点，在图③中B₁，B₂…B₉；C₁C₂…C₉分别是AB、AC的10等分点，则B₁C₁+B₂C₂+…+B₉C₉的值是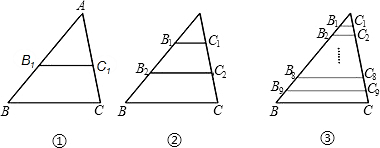

 

．

Answer 1

分析：先根据三角形中位线定理、平行线分线段成比例定理找出题中的规律，然后根据规律求解．

解答：解：当B₁、C₁是AB、AC的中点时，B₁C₁=

1

2

BC；
当B₁，B₂，C₁，C₂分别是AB，AC的三等分点时，B₁C₁+B₂C₂=

1

3

BC+

2

3

BC；
…
当B₁，B₂，C₁，…，C_n分别是AB，AC的n等分点时，
B₁C₁+B₂C₂+…+B_n-1B_n-1=

1

n

BC+

2

n

BC+…+

n-1

n

BC=

n(n-1)

2n

BC=5（n-1）；
当n=10时，5（n-1）=45；
故B₁C₁+B₂C₂+…+B₉C₉的值是45．
故答案为45．

点评：解答此类规律型问题，通常要根据简单的例子找出一般化规律，然后根据规律来来特定的值．